题目内容
9.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的焦距为2,点Q($\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$,0)在直线l:x=3上.(1)求椭圆C的标准方程;
(2)若O为坐标原点,P为直线l上一动点,过点P作直线与椭圆相切点于点A,求△POA面积S的最小值.
分析 (1)由题意可知:c=1,由Q($\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$,0)在直线l:x=3上.即可求得a和b的值,求得椭圆方程;
(2)将直线方程代入椭圆方程,△=0,即可求得A点坐标,根据三角形的面积公式,利用导数与函数单调性的关系,即可求得△POA面积S的最小值.
解答 解:(1)椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的焦距为2,则2c=2,c=1,又点Q($\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$,0)在直线l:x=3上,
∴a2=3,∴b2=a2-c2=2.
∴椭圆C的标准方程是$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$;
(2)由题意直线l的斜率存在,设直线l的方程为y=kx+m,设P(3,y0),A(x1,y1).
由$\left\{\begin{array}{l}{y=kx+m}\\{2{x}^{2}+3{y}^{2}=6}\end{array}\right.$,整理得(2+3k2)x2+6kmx+3m2-6=0,由△=24(2+3k2-m2)=0,则2+3k2=m2,
x1=-$\frac{3km}{2+3{k}^{2}}$,则y1=$\frac{2m}{2+3{k}^{2}}$,y0=kx+m.
由2+3k2=m2,则m=±$\sqrt{2+3{k}^{2}}$.
当m=$\sqrt{2+3{k}^{2}}$.时,△POA面积S△OPA=$\frac{3}{2}$丨k+$\sqrt{2+3{k}^{2}}$丨,又$\sqrt{2+3{k^2}}>\sqrt{3{k^2}}>|k|$,k+$\sqrt{2+3{k}^{2}}$>0,
∴S△OPA=$\frac{3}{2}$(k+$\sqrt{2+3{k}^{2}}$).
令f(k)=$\frac{3}{2}$(k+$\sqrt{2+3{k}^{2}}$),k∈R,则f′(k)=$\frac{3}{2}$(1+$\frac{3k}{\sqrt{2+3{k}^{2}}}$)=$\frac{3}{2}$($\frac{\sqrt{2+3{k}^{2}}+3k}{\sqrt{2+3{k}^{2}}}$),
由f′(k)=0,得k=-$\frac{\sqrt{3}}{3}$,f(k)在(-∞,-$\frac{\sqrt{3}}{3}$)上单调递减,在(-$\frac{\sqrt{3}}{3}$,+∞)单调递增,
∴f(k)min=f(-$\frac{\sqrt{3}}{3}$)=$\sqrt{3}$.即当l的斜率为-$\frac{\sqrt{3}}{3}$时,△OPA面积S的最小值为$\sqrt{3}$.
同理当m=-$\sqrt{2+3{k}^{2}}$.时,S△OPA=$\frac{3}{2}$(-k+$\sqrt{2+3{k}^{2}}$).当l的斜率为$\frac{\sqrt{3}}{3}$时,△OPA面积S的最小值为$\sqrt{3}$.
综上,△OPA面积S的最小值为$\sqrt{3}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查导数与函数单调性的关系,考查计算能力,属于中档题.

| A. | x1+x2-1>0 | B. | x1+x2-1<0 | C. | x2-x1>0 | D. | x2-x1<0 |
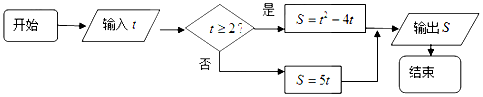
| A. | 10 | B. | 5 | C. | 0 | D. | -5 |
| A. | $({0,\frac{3}{4}})$ | B. | $({0,\frac{1}{4}}]$ | C. | $[{\frac{1}{4},\frac{3}{4}}]$ | D. | $[{\frac{3}{4},+∞})$ |
| A. | 函数$f(x)=sin\sqrt{x}$不是周期函数. | |
| B. | 函数$f(x)=sin\frac{1}{x}$不是周期函数. | |
| C. | 函数f(x)=sin|x|不是周期函数. | |
| D. | 函数f(x)=|sinx|+|cosx|的最小正周期为π. |