题目内容
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1(n∈N*).
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出证明.
(1)当n=1时,方程x2-a1x-a1=0有一根为S1-1=a1-1,
∴(a1-1)2-a1(a1-1)-a1=0,
解得a1=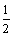 .当n=2时,方程x2-a2x-a2=0有一根为S2-1=a1+a2-1=a2-
.当n=2时,方程x2-a2x-a2=0有一根为S2-1=a1+a2-1=a2-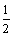 ,
,
∴(a2-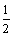 )2-a2(a2-
)2-a2(a2-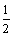 )-a2=0,解得a2=
)-a2=0,解得a2=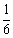 .
.
(2)由题意知(Sn-1)2-an(Sn-1)-an=0,
当n≥2时,an=Sn-Sn-1,代入上式整理得
SnSn-1-2Sn+1=0,解得Sn=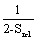 .
.
由(1)得S1=a1=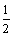 ,S2=a1+a2=
,S2=a1+a2=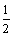 +
+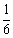 =
=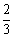 .
.
猜想Sn=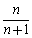 (n∈N*).
(n∈N*).
下面用数学归纳法证明这个结论.
①当n=1时,结论成立.
②假设n=k(k∈N*,k≥1)时结论成立,即Sk=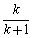 ,当n=k+1时,
,当n=k+1时,
Sk+1=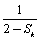 =
=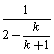 =
=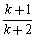 .
.
即当n=k+1时结论成立.
由①②知Sn=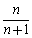 对任意的正整数n都成立.
对任意的正整数n都成立.

某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2—6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2—6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从下表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附:我国2010年和2011年2—6月的CPI数据(单位:百分点.注:1个百分点=1%)
| 年份 | 2月 | 3月 | 4月 | 5月 | 6月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 2.9 |
| 2011 | 4.9 | 5.0 | x | y | z |
 的渐近线方程为
的渐近线方程为 ,则
,则 的值为________
的值为________ <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
= =(k+1)+1,∴当n=k+1时,不等式成立,则上述证法( )
=(k+1)+1,∴当n=k+1时,不等式成立,则上述证法( )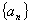 的通项公式
的通项公式 ,记
,记 ,试通过计算
,试通过计算 的值,推测出
的值,推测出
 ,2;
,2; ,3;
,3; ,4;
,4; ,5;
,5; ,4;
,4; ,2.则样本在
,2.则样本在 上的频率是 .
上的频率是 . 满足
满足 ,则
,则 的最小值为
的最小值为  ,若
,若 的实部和虚部互为相反数,则实数
的实部和虚部互为相反数,则实数 的值为( )
的值为( ) C. -
C. - 面积的最小值.
面积的最小值.