题目内容
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(Ⅱ)设C、D为直线l1、l2与直线x = 4的交点,求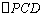 面积的最小值.
面积的最小值.
【解析】(Ⅰ)设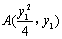 ,
, 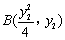 (
(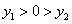 ).
).
易知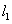 斜率存在,设为
斜率存在,设为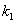 ,则
,则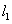 方程为
方程为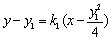 .
.
由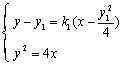 得,
得,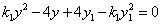 …………… ①
…………… ①
由直线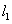 与抛物线
与抛物线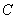 相切,知
相切,知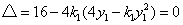 .
.
于是,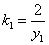 ,
,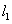 方程为
方程为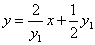 .
.
同理,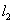 方程为
方程为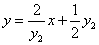 .
.
联立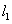 、
、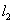 方程可得点
方程可得点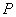 坐标为
坐标为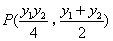 ,
,
∵ 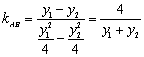 ,
,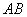 方程为
方程为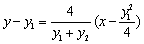 ,
,
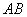 过抛物线
过抛物线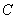 的焦点
的焦点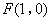 .
.
 ∴
∴ 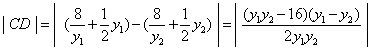 .
.
∴ 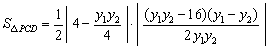 .
.
设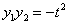 (
(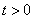 ),
),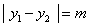 ,
,
由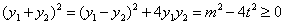 知,
知,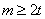 ,当且仅当
,当且仅当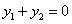 时等号成立.
时等号成立.
∴ 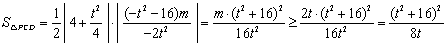 .
.
设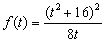 ,则
,则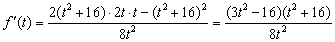 .
.
∴ 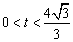 时,
时,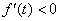 ;
;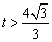 时,
时,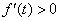 .
.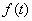 在区间
在区间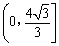 上为减函数;
上为减函数;
在区间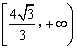 上为增函数.
上为增函数.
∴ 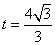 时,
时,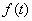 取最小值
取最小值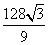 .
.
∴ 当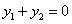 ,
,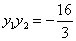 ,
,
即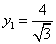 ,
,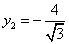 时,
时,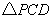 面积取最小值
面积取最小值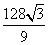 . ………… 13分
. ………… 13分

练习册系列答案
相关题目
 时,从“
时,从“ 到
到 ”左边需增加的代数式是______________________.
”左边需增加的代数式是______________________.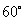 ,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有
,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有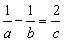 ,则称a、 b、c是调和的;若满a + c = 2b足,则称a、b、c是等差的.若集合P中元素a、b、c既是调和的,又是等差的,则称集合P为“好集”.若集合
,则称a、 b、c是调和的;若满a + c = 2b足,则称a、b、c是等差的.若集合P中元素a、b、c既是调和的,又是等差的,则称集合P为“好集”.若集合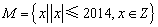 ,集合
,集合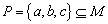 .则
.则 为等比数列,
为等比数列, 是它的前n项和,若
是它的前n项和,若
 ,且
,且 与
与 的等差中项为
的等差中项为 ,则
,则 =
=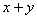 的值为
的值为 

 .
.
 .
.
 .
.
 .
.