题目内容
已知函数f(x)=sinx+cos(x-
),求函数f(x)的单调递减区间.
| π |
| 6 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:首先通过恒等变换不函数变形成正弦型函数,进一步求出单调区间.
解答:
解:(1)已知:f(x)=sinx+cos(x-
)=sinx+
cosx+
sinx=
sin(x+
) …(1分)
令:
+2kπ≤x+
≤
+2kπ(k∈Z)
解得:
+2kπ≤x≤
+2kπ(k∈Z)
所以:函数的单调递减区间为:[
+2kπ,
+2kπ](k∈Z)
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
令:
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解得:
| π |
| 3 |
| 4π |
| 3 |
所以:函数的单调递减区间为:[
| π |
| 3 |
| 4π |
| 3 |
点评:本题考查的知识点:三角函数关系式的恒等变换,正弦型函数的单调区间的求法.

练习册系列答案
相关题目
已知图1、图2分别表示A、B两城市某月1日至6日当天最低气温的数据折线图(其中横轴n表示日期,纵轴x表示气温),记A、B两城市这6天的最低气温平均数分别为
和
,标准差分别为sA和sB,则它们的大小关系是( )
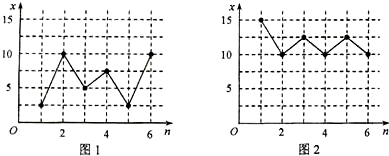
. |
| xA |
. |
| xB |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的公共弦长为( )
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
若平面
,
满足|
+
|=1,
+
平行于y轴,
=(2,-1),则
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| A、(-1,1) |
| B、(-2,2) |
| C、(-1,1)或(-3,1) |
| D、(-2,2)或(-2,0) |