题目内容
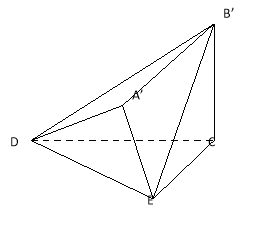
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.

(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) (1)![]() ,(2)
,(2)![]() .
.
【解析】试题分析:(Ⅰ)利用中位线定理得出DE//AB,即可证得;
(Ⅱ)(1)在![]() 中,利用勾股定理运算即可;
中,利用勾股定理运算即可;
(2)以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系,利用向量求解线面角即可.
试题解析:
(Ⅰ)证明:连结![]() 交
交![]() 于E,连结DE,
于E,连结DE,
∵D、E分别为![]() 和
和![]() 的中点,
的中点,
∴DE//AB,
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴AB//平面CDB1;
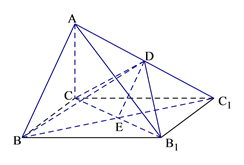
(Ⅱ)(1)∵AC⊥平面BCC1B1, ![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
在![]() ,∵BC=1,
,∵BC=1, ![]() ,
,
∴![]() ;
;
【注:以上加灰色底纹的条件不写不扣分!】
(2)依题意知AC、BC、CC1两两互相垂直,以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系如图示,
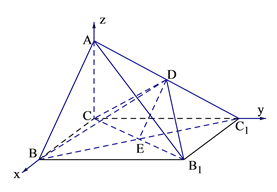
易得![]() ,
, ![]() ,
,
![]() ,
, 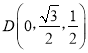 ,
,
故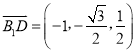 ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() 得
得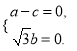 令
令![]() 得
得![]() ,
,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则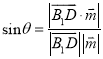
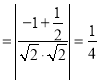 ,
,
即![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
【其它解法请参照给分,如先用体积法求出点D到平面ABB1的距离![]() ,(10分)再用公式
,(10分)再用公式![]() 算
算![]() 与平面
与平面![]() 所成角的正弦值(12分)】
所成角的正弦值(12分)】

【题目】2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(![]() ,表示丢失的数据)
,表示丢失的数据)
无意愿 | 有意愿 | 总计 | |
男 |
|
| 40 |
女 | 5 |
|
|
总计 | 25 |
| 80 |
(1)求出![]() 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据: 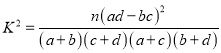 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
【题目】某市英才中学的一个社会实践调查小组,在对中学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对收回的120份有效问卷进行统计,得到如下![]() 列联表:
列联表:
做不到光盘 | 能做到光盘 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现已按是否能做到光盘分层从45份女生问卷中抽取9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过![]() ,那么根据临界值表最精确的
,那么根据临界值表最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量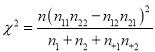 ,其中
,其中![]() .
.
独立性检验临界表:
|
|
|
|
|
|
|
|
|
|
|
|