题目内容

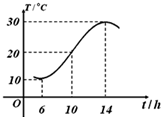
如图，某地一天从6～14时的温度变化曲线近似满足函数：y=Asin（ωx+φ）+B．则中午12点时最接近的温度为（　　）
A．26°CB．27°CC．28°CD．29°C
精英家教网
不妨令A＞0，B＞0，
则由
A+B=30
B-A=10
得：A=10，B=20°C；
又
T
2
=14-6=8，
∴T=16=
2π
|ω|
，
∴|ω|=
π
8
，不妨取ω=
π
8
．
由图可知，6×
π
8
+φ=2kπ-
π
2
（k∈Z），
∴φ=2kπ-
5π
4
，不妨取φ=
3π
4
．
∴曲线的近似解析式为：y=10sin（
π
8
x+
3π
4
）+20，
∴中午12点时最接近的温度为：y=10sin（
π
8
×12+
3π
4
）+20°C=10sin
9π
4
+20°C=20+10sin
π
4
=5
2
+20°C≈27°C．
故选B．
练习册系列答案
相关题目
精英家教网如图，某地一天从6-14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，则b=
 
；该段曲线的函数解析式是
 
．
精英家教网如图，某地一天从6时至14时的温度变化曲线近似满足函数y=Asin（ωx+∅）+b．
（1）求这段时间的最大温差；
（2）写出这段时间的函数解析式．
精英家教网如图，某地一天从6～14时的温度变化曲线近似满足函数：y=Asin（ωx+φ）+b，则A、ω、φ、b分别是（　　）
A、A=10、ω=
π
8
、φ=
3π
4
、b=20
B、A=20、ω=
π
4
、φ=
3π
4
、b=10
C、A=30、ω=
π
8
、φ=
3π
4
、b=10
D、A=10、ω=
1
8
、φ=
3π
4
、b=20
（2011•佛山二模）如图，某地一天从6～14时的温度变化曲线近似满足函数：y=Asin（ωx+φ）+B．则中午12点时最接近的温度为（　　）

 

 
如图，某地一天从6时至14时的温度变化曲线近似满足函数．

   （Ⅰ）求这段时间的最大温差；

   （Ⅱ）写出这段曲线的函数解析式．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网