题目内容
7．已知点P（x，y）的坐标满足条件$\left\{\begin{array}{l}x+y≤4\\ y≥x\\ x≥1\end{array}\right.$，则$\sqrt{{x^2}+{y^2}}$的最大值为$\sqrt{10}$．分析 作出平面区域，$\sqrt{{x^2}+{y^2}}$表示区域内的点与原点的距离，数形结合可得．
解答 
解：作出条件$\left\{\begin{array}{l}x+y≤4\\ y≥x\\ x≥1\end{array}\right.$所对应的平面区域（如图△ABC），
$\sqrt{{x^2}+{y^2}}$表示区域内的点与原点的距离，
数形结合可得区域内的点A（1，3）满足题意，
由距离公式计算可得$\sqrt{{x^2}+{y^2}}$的最大值为$\sqrt{10}$，
故答案为：$\sqrt{10}$．
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
15．若cosθ=$\frac{3}{5}$（-$\frac{π}{2}$＜θ＜0），则cos（θ-$\frac{π}{6}$）的值是（ ）
| A． | $\frac{3\sqrt{3}±4}{10}$ | B． | $\frac{4±3\sqrt{3}}{10}$ | C． | $\frac{3\sqrt{3}-4}{10}$ | D． | $\frac{3\sqrt{3}+4}{10}$ |
12．
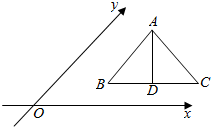如图所示的是水平放置的三角形的直观图，D为△ABC中BC的中点，则原图形中的AB，AD，AC三条线段中（ ）
如图所示的是水平放置的三角形的直观图，D为△ABC中BC的中点，则原图形中的AB，AD，AC三条线段中（ ）| A． | 最长的是AB，最短的是AC | B． | 最长的是AC，最短的是AB | ||
| C． | 最长的是AB，最短的是AD | D． | 最长的是AC，最短的是AD |