题目内容
已知椭圆C1:
+
=1,双曲线C2:
-
=1(m,n>0),椭圆C1的焦点和长轴端点分别是双曲线C2的顶点和焦点,则双曲线C2的渐近线必经过点( )
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
A、(
| ||||
B、(2,
| ||||
C、(
| ||||
D、(
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆C1的焦点和长轴端点,可得是双曲线C2的顶点和焦点,从而可得双曲线C2的渐近线,代入验证可得结论.
解答:
解:∵椭圆C1:
+
=1,
∴椭圆C1的焦点是(±1,0),长轴端点是(±2,0),
∴双曲线C2的顶点是(±1,0),焦点是(±2,0),
∴双曲线C2的渐近线方程为y=±
x,
∴双曲线C2的渐近线必经过点(
,-3)
| x2 |
| 4 |
| y2 |
| 3 |
∴椭圆C1的焦点是(±1,0),长轴端点是(±2,0),
∴双曲线C2的顶点是(±1,0),焦点是(±2,0),
∴双曲线C2的渐近线方程为y=±
| 3 |
∴双曲线C2的渐近线必经过点(
| 3 |
点评:本题考查椭圆、双曲线的几何性质,考查学生的计算能力,正确确定椭圆C1的焦点和长轴端点坐标是关键.

练习册系列答案
相关题目
已知全集U={0,1,2,3,4},集合A={1,2},B={2,3,4},则B∩∁UA的子集个数有( )
| A、2 | B、4 | C、8 | D、16 |
设F是双曲线
-
=1的右焦点,双曲线两渐近线分另.为l1,l2过F作直线l1的垂线,分别交l1,l2于A,B两点.若OA,AB,OB成等差数列,且向量
与
同向,则双曲线的离心 率e的大小为( )
| x2 |
| a2 |
| y2 |
| b2 |
| BF |
| FA |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
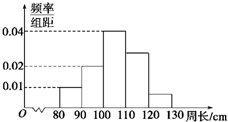 为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )| A、3000 | B、6000 |
| C、7000 | D、8000 |
设集合S={x|x2-2x-3≤0},T={x|-1<x≤4,x∈Z},则S∩T等于 ( )
| A、{x|0<x≤3,x∈Z} |
| B、{x|0≤x≤4,x∈Z} |
| C、{x|-1≤x≤0,x∈Z} |
| D、{x|-1<x≤3,x∈Z} |
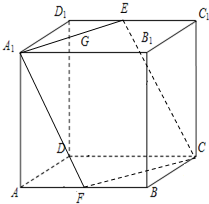 如图,在正方体ABCD-A1B1C1D1中,E、F分别为C1D1与AB的中点,则A1B1与截面A1ECF所成角的大小为
如图,在正方体ABCD-A1B1C1D1中,E、F分别为C1D1与AB的中点,则A1B1与截面A1ECF所成角的大小为