题目内容
已知函数f(x)=x3+2x-sinx,(x∈R)
(1)证明:函数f(x)是R上的单调递增函数;
(2)解关于x的不等式f(ax2-x)+f(1-ax)<0,其中a∈R.
(1)证明:函数f(x)是R上的单调递增函数;
(2)解关于x的不等式f(ax2-x)+f(1-ax)<0,其中a∈R.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)求函数 导数,利用导数即可证明函数f(x)是R上的单调递增函数;
(2)判断函数的奇偶性和单调性,将不等式进行转化即可解不等式.
(2)判断函数的奇偶性和单调性,将不等式进行转化即可解不等式.
解答:
解:(1)函数的f(x)的导数f′(x)=3x2+2-cosx,
∵3x2≥0,2-cosx>0,
∴f′(x)>0,故函数f(x)是R上的单调递增函数.
(2)∵f(-x)=-x3-2x+sinx=-(x3+2x-sinx)=-f(x),
∴f(x)为奇函数,
则不等式等价为f(ax2-x)<-f(1-ax)=f(ax-1),
则ax2-x<ax-1,
整理得ax2-(a+1)x+1<0,
即(ax-1)(x-1)<0,
若a=0,则不等式等价为x-1>0,解得x>1.
若a<0,则不等式等价为 a(x-
)(x-1)<0,
即(x-
)(x-1)>0,此时不等式的解集为(-∞,
)∪(1,+∞),
若a>0,不等式等价为 (x-
)(x-1)<0,
若a=1,则不等式的解集为∅.
若0<a<1,不等式的解集为(1,
),
若a>1,不等式的解集为(
,1).
∵3x2≥0,2-cosx>0,
∴f′(x)>0,故函数f(x)是R上的单调递增函数.
(2)∵f(-x)=-x3-2x+sinx=-(x3+2x-sinx)=-f(x),
∴f(x)为奇函数,
则不等式等价为f(ax2-x)<-f(1-ax)=f(ax-1),
则ax2-x<ax-1,
整理得ax2-(a+1)x+1<0,
即(ax-1)(x-1)<0,
若a=0,则不等式等价为x-1>0,解得x>1.
若a<0,则不等式等价为 a(x-
| 1 |
| a |
即(x-
| 1 |
| a |
| 1 |
| a |
若a>0,不等式等价为 (x-
| 1 |
| a |
若a=1,则不等式的解集为∅.
若0<a<1,不等式的解集为(1,
| 1 |
| a |
若a>1,不等式的解集为(
| 1 |
| a |
点评:本题主要考查不等式的求解以及函数单调性的判断和证明,利用导数以及一元二次不等式的解法是解决本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、命题“若p或q”为真命题,则p,q中至少有一个为真命题 |
| B、命题“?x0∈R,x02+x0-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、命题“若x=y,则sinx=siny”的逆否命题为假命题 |
| D、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
已知-
<α<β<
,则α-β的范围是( )
| π |
| 6 |
| 2π |
| 3 |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
已知函数g(x)=ax+a,f(x)=
,若对任意的x1∈[-2,2],存在x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是( )
|
A、[-
| ||
B、[-
| ||
| C、(0,1] | ||
| D、(-∞,1] |
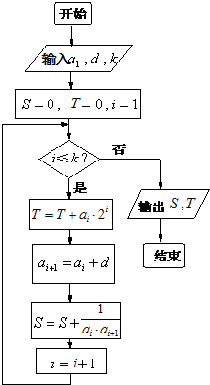 如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是
如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是 设y=f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,2),斜率为-1的一条射线,又当x∈[-1,0]时,y=f(x)的图象是顶点在(0,2),且过点(-1,1)的一段抛物线.
设y=f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,2),斜率为-1的一条射线,又当x∈[-1,0]时,y=f(x)的图象是顶点在(0,2),且过点(-1,1)的一段抛物线.