题目内容
求下列函数的单调区间,并指出其单调性.(1)f(x)=x3;
(2)f(x)=2x3-9x2+12x-3;
(3)f(x)=lnsinx.
解:(1)∵f′(x)=3x2,∴当x≠0时,f′(x)>0.当x=0时,f′(x)=0.又当x>0时f(x)>0,x<0时f(x)<0,x=0时f(x)=0,根据函数的连续性知f(x)在(-∞,+∞)上是增函数,即y= x3的增区间为(-∞,+∞).
(2)∵f′(x)=6x2-18x+12,由f′(x)<0得1<x<2,由f′(x)>0得x<1或x>2,故f(x)的增区间为(-∞,1)及(2,+∞),减区间为(1,2).
(3)函数f(x)的定义域为2kπ<x<2kπ+π(k∈Z).
∵f′(x)= ![]() =cotx,由f′(x)>0及函数的定义域得2kπ<x<2kπ+
=cotx,由f′(x)>0及函数的定义域得2kπ<x<2kπ+![]() (k∈Z),
(k∈Z),
由f′(x)<0及函数的定义域得2kπ+![]() <x<2kπ+π(k∈Z),
<x<2kπ+π(k∈Z),
故该函数的单调增区间为(2kπ,2kπ+![]() )(k∈Z),
)(k∈Z),
减区间为(2kπ+![]() ,2kπ+π)(k∈Z).
,2kπ+π)(k∈Z).

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;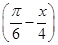 .
.