题目内容
19.求函数f(x)=$\frac{{x}^{2}+2x+3}{{x}^{2}+x+2}$在区间[0,+∞)上的最大值.分析 先化简,再求导,得到函数f(x)的单调性,即可求出最值.
解答 解:f(x)=$\frac{{x}^{2}+2x+3}{{x}^{2}+x+2}$=$\frac{{x}^{2}+x+2+x+1}{{x}^{2}+x+2}$=1+$\frac{x+1}{{x}^{2}+x+2}$,
∴f′(x)=$\frac{{x}^{2}+x+2-(x+1)(2x+1)}{({x}^{2}+x+2)^{2}}$=$\frac{-{x}^{2}-2x+1}{({x}^{2}+x+2)^{2}}$,
令f′(x)=0,解得x=$\sqrt{2}$-1,
当f′(x)>0时,即x∈[0,$\sqrt{2}$-1),函数单调递增,
当f′(x)<0时,即x∈[$\sqrt{2}$-1,+∞),函数单调递减,
∴f(x)max=f($\sqrt{2}$-1)=1+$\frac{\sqrt{2}-1+1}{(\sqrt{2}-1)(\sqrt{2}-1+1)+2}$=1+$\frac{2\sqrt{2}+1}{6}$=$\frac{2\sqrt{2}+7}{6}$
点评 本题考查了利用导数和函数最值得关系,关键是判断函数的单调性,属于中档题.

练习册系列答案
相关题目
14.${∫}_{1}^{2}$(x+2x)dx等于( )
| A. | (x+2x)|${\;}_{1}^{2}$ | B. | (x2+2xln2)|${\;}_{1}^{2}$ | ||
| C. | ($\frac{{x}^{2}}{2}$+2x)|${\;}_{1}^{2}$ | D. | ($\frac{{x}^{2}}{2}$+$\frac{{2}^{x}}{ln2}$)|${\;}_{1}^{2}$ |
8.方程3x+4x=5x解的情况是( )
| A. | 有且只有一个根2 | B. | 不仅有根2还有其他根 | ||
| C. | 有根2和另一个负根 | D. | 有根2和另一个正根 |
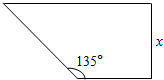 某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).
某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).