题目内容
20. 某校高二学生有800名,从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校高二学生有800名,从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100](Ⅰ)求图中α的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分、中位数、众数;(精确到个位数)
(Ⅲ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求推测高二这800名学生中数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
分析 (Ⅰ)由频率和为1,列出方程求出α的值;
(Ⅱ)利用频率分布直方图求出平均数、中位数与众数;
(Ⅲ)根据表格,求出学生的语文成绩对应的人数,即可得出数学成绩对应的人数是多少.
解答 解:(Ⅰ)由频率分布直方图知,
(0.04+0.03+0.02+2α)×10=1,
解得α=0.005;…(2分)
(Ⅱ)55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73,
所以平均分为73;…(4分)
由于直方图中中位数两侧的面积相等,即频率相等,
前两组的频率和为0.45,前三组的频率和为0.75,
所以中位数位于第3组内,设中位数为x,
(x-70)×0.03+0.45=0.5
x≈72; …(6分)
小组[60,70)的矩形图最高,
所以众数应为$\frac{60+70}{2}$=65; …(8分)
(Ⅲ)分别求出100名学生中,语文成绩在[50,60),[60,70),[70,80),[80,90)的人数依次为0.05×100=5,0.4×100=40,0.3×100=30,0.2×100=20;
所以100名学生中数学成绩在[50,60),[60,70),[70,80),[80,90)的人数依次为:
5,20,40,25;
所以数学成绩在[50,90)之外的人数有100-(5+20+40+25)=10(人);
从而推测高二这800名学生中数学成绩在[50,90)之外的人数为80(人).…(12分)
点评 本题考查了频率分布直方图的应用问题,也考查了平均数、众数与中位数的计算问题,是基础题目.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.曲线f(x)=exlnx+$\frac{{2{e^{x-1}}}}{x}$在点(1,f(1))处的切线方程为( )
| A. | ex-y+2-e=0 | B. | ex+y+2-e=0 | C. | ex-y+2+e=0 | D. | ex+y+2+e=0 |
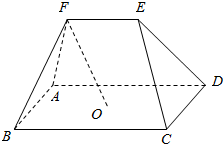 如图,在五面体ABCDE中,点O是平行四边形ABCD的对角线的交点,棱$EF\underline{\underline{∥}}\frac{1}{2}BC$
如图,在五面体ABCDE中,点O是平行四边形ABCD的对角线的交点,棱$EF\underline{\underline{∥}}\frac{1}{2}BC$