题目内容
已知三条直线:l1:2x-y+a=0(a>0);l2:-4x+2y+ 1=0;l3:x+y-1=0,且l1与l2间的距离是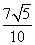 .
.
(1)求a的值;
(2)能否找到一点P,使P同时满足下列三个条件:
①点P在第一象限;
②点P到l1的距离是点P到l2的距离的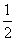 ;
;
③点P到l1的距离与点P到l3的距离之比是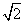 ∶
∶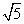 .若能,求点P的坐标;若不能,说明理由.
.若能,求点P的坐标;若不能,说明理由.
解 (1)直线l2:2x-y-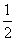 =0,所以两条平行线l1与l2间的距离为d=
=0,所以两条平行线l1与l2间的距离为d=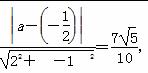
所以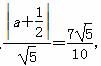 ,即
,即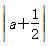 =
=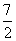 ,又a>0,解得a=3.
,又a>0,解得a=3.
(2)假设存在点P,设点P(x0,y0),若P点满足条件②,则P点在与l1,l2平行的直线l′:2x-y+c=0上,且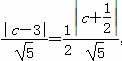 ,即c=
,即c=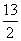 或
或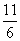 ,
,
所以2x0-y0+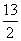 =0或2x0-y0+
=0或2x0-y0+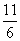 =0;
=0;
若P点满足条件③,由点到直线的距离公式,
有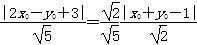
即|2x0-y0+3|=|x0+y0-1|,
所以x0-2y0+4=0或3x0+2=0;
由于P在第一象限,
所以3x0+2=0不可能.
联立方程2x0-y0+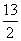 =0和x0-2y0+4=0,
=0和x0-2y0+4=0,
解得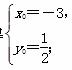
联立方程2x0-y0+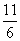 =0和x0-2y0+4=0,
=0和x0-2y0+4=0,
解得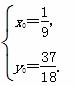 所以存在P
所以存在P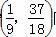 同时满足三个条件.
同时满足三个条件.

练习册系列答案
相关题目
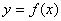 图象上的点到坐标原点距离的最小值叫做函数
图象上的点到坐标原点距离的最小值叫做函数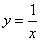 的“中心距离”大于1;
的“中心距离”大于1; 的“中心距离”大于1;
的“中心距离”大于1;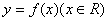 与
与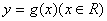 的“中心距离” 相等,则函数
的“中心距离” 相等,则函数 至少有一个零点.
至少有一个零点.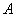 .①②
.①② 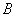 .②③
.②③ 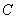 .①③
.①③ 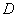 .①
.①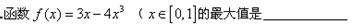
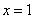 是函数
是函数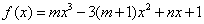 的一个极值点,其中
的一个极值点,其中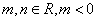 ,
,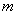 与
与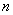 的关系式; (2)求
的关系式; (2)求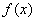 的单调区间;
的单调区间;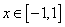 时,函数
时,函数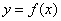 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,则该圆的标准方程是________.
,则该圆的标准方程是________.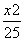 +
+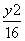 =1的左、右焦点,P为椭 圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的 距离为 ( ).
=1的左、右焦点,P为椭 圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的 距离为 ( ).