题目内容
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() =1(a>b>0)的左右焦点分别为F1,F2,焦距为2,一条准线方程为x=2.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.
=1(a>b>0)的左右焦点分别为F1,F2,焦距为2,一条准线方程为x=2.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.
(1)求椭圆C的方程;
(2)若点P的坐标为(0,b),求过点P,Q,F2三点的圆的方程;
(3)若![]() =
=![]() ,且λ∈[
,且λ∈[![]() ],求
],求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)通过焦距以及准线方程,求出a,c,然后求解b,得到椭圆方程.
(2)求出三点坐标,设出圆的一般方程,然后求解即可.
(3)求出P的坐标,代入椭圆方程,通过向量的数量积结合基本不等式求解即可.
(1)由题意得 ,解得c=1,a2=2,所以b2=a2-c2=1.
,解得c=1,a2=2,所以b2=a2-c2=1.
所以椭圆的方程为![]() .
.
(2)因为P(0,1),F1(-1,0),所以PF1的方程为x-y+1=0.
由 解得
解得![]() 或
或 所以Q点的坐标为
所以Q点的坐标为![]() .
.
设过P,Q,F2三点的圆的方程为x2+y2+Dx+Ey+F=0,
则
解得
所以圆的方程为![]() .
.
(3)设P(x1,y1),Q(x2,y2),则![]() .
.
因为![]() ,所以
,所以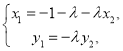
所以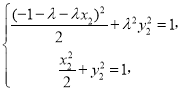 ,解得
,解得![]() .
.
所以![]()
=![]()
=![]() .
.
因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即λ=1时取等号,
,即λ=1时取等号,
所以![]() .即
.即![]() 最大值为
最大值为![]() .
.

练习册系列答案
相关题目