题目内容
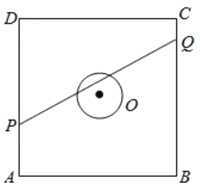
【题目】如图，正方形
的边长为
米，圆
的半径为
米，圆心是正方形的中心，点
、
分别在线段
、
上，若线段
与圆有公共点，则称点在点的“盲区”中，已知点以
米/秒的速度从
出发向
移动，同时，点以米/秒的速度从
出发向
移动，则在点从移动到的过程中，点在点的盲区中的时长约________秒（精确到
）．
【答案】
【解析】
以点
为坐标原点，建立如图所示的平面直角坐标系，求出点
、
的坐标和直线
的方程以及圆的方程，利用点到直线的距离公式，以及直线和圆相交的条件下，解不等式即可得出所求时长.
以点为坐标原点，建立如下图所示的平面直角坐标系：
可设点
，
，
可得出直线的方程为
，圆的方程为
，
由直线与圆有公共点，可得
，化为
，
解得
，而
，
因此，点在点的盲区中的时长约为秒.
故答案为：.
练习册系列答案
相关题目
