Question

【题目】已知双曲线的一个焦点是，且

（1）求双曲线的方程

（2）设经过焦点的直线的一个法向量为，当直线与双曲线的右支相交于不同的两点时，求实数的取值范围

（3）设（2）中直线与双曲线的右支相交于两点，问是否存在实数，使得为锐角？若存在，请求出的范围；若不存在，请说明理由

Answer 1

【答案】（1）；（2）或；（3）不存在，证明见解析

【解析】

（1）直接根据题意计算得到得到答案.

（2）计算渐近线方程为，根据直线方程与渐近线的关系得到答案.

（3）假设存在，为锐角，即，利用韦达定理得到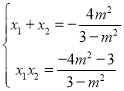

，解得，不成立.

（1）双曲线的一个焦点是，且

则 解得 故双曲线方程为

（2）渐近线方程为：

经过焦点的直线的一个法向量为，则直线方程为：

直线与双曲线的右支相交于不同的两点

则满足或，解得：或

（3）假设存在，则为锐角，即 ，设

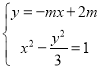得到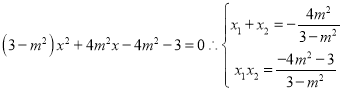

代入化简得到： 即

这与或矛盾，假设不成立.

故不存在这样的