题目内容
已知椭圆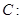
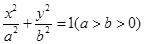 的离心率为
的离心率为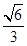 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为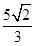 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知动直线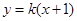 与椭圆
与椭圆 相交于
相交于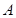 、
、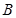 两点. ①若线段
两点. ①若线段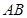 中点的横坐标为
中点的横坐标为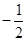 ,求斜率
,求斜率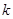 的值;②若点
的值;②若点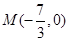 ,求证:
,求证: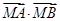 为定值.
为定值.
(Ⅰ)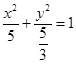 ;(Ⅱ)①
;(Ⅱ)① ;②
;② .
.
解析试题分析:(Ⅰ)根据已知条件可设椭圆方程为: ,则有
,则有 ,
,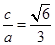 ,
, ,求解即可得到
,求解即可得到 和
和 的值,将对应的解代入椭圆方程即可;(Ⅱ)①将直线方程
的值,将对应的解代入椭圆方程即可;(Ⅱ)①将直线方程 代入椭圆方程求得,
代入椭圆方程求得, ,求得
,求得 、
、 两点的横坐标之和为
两点的横坐标之和为 ,由已知条件“
,由已知条件“ 中点的横坐标为
中点的横坐标为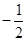 ”,得到
”,得到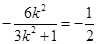 ,从而解得
,从而解得 的值;
的值;
②根据①的 、
、 两点的坐标求得
两点的坐标求得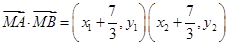 ③,结合
③,结合 、
、 两点坐标满足直线方程
两点坐标满足直线方程 ,将③式化简整理得
,将③式化简整理得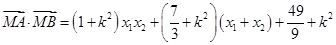 ,再由①中的根与系数的关系:
,再由①中的根与系数的关系: ,
,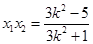 ,代入化简即可.
,代入化简即可.
试题解析:(Ⅰ)因为 满足
满足 ,
,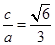 ,
, ,
,
解得 ,
, ,
,
则椭圆方程为: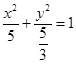 . 3分
. 3分
(Ⅱ)①将 代入
代入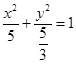 中得,
中得, ,
,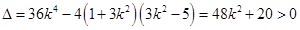 ,
,
设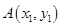 ,
, ,则
,则 ,
,
因为 中点的横坐标为
中点的横坐标为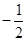 ,所以
,所以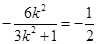 ,
,
解得 . 6分
. 6分
②由①知, ,
,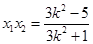 ,
,
所以

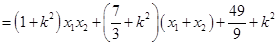
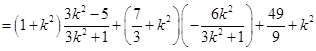
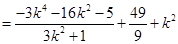
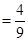 . 12分
. 12分
考点:1.椭圆的标准方程;2.椭圆的性质;3.方程的根与系数的关系;4.中点坐标公式;5.平面向量的数量积

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的方程为
的方程为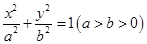 ,双曲线
,双曲线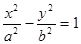 的两条渐近线为
的两条渐近线为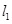 、
、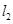 .过椭圆
.过椭圆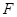 作直线
作直线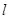 ,使
,使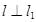 ,又
,又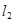 交于点
交于点 ,设
,设 、
、 .
.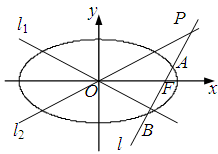
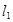 与
与 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆 的最大值.
的最大值. 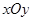 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为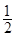 的椭圆E的一个焦点为圆
的椭圆E的一个焦点为圆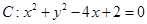 的圆心.
的圆心. ,当直线
,当直线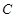 相切时,求P点坐标.
相切时,求P点坐标.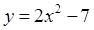 ,求曲线过点
,求曲线过点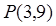 的切线方程。
的切线方程。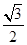 的椭圆过点
的椭圆过点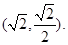
 与该椭圆交于P,Q两点,满足直线
与该椭圆交于P,Q两点,满足直线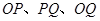 的斜率依次成等比数列,
的斜率依次成等比数列,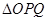 面积的取值范围.
面积的取值范围. ,且和直线
,且和直线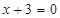 相切,
相切,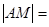 5,求M点的坐标.
5,求M点的坐标. :
: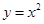 .过点
.过点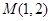 的直线
的直线 交
交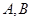 两点.抛物线
两点.抛物线 处的切线与在点
处的切线与在点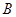 处的切线交于点
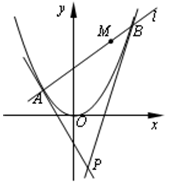
处的切线交于点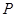 .
.
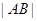 ;
;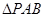 面积的最小值.
面积的最小值.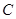 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 。
。 为斜率的直线
为斜率的直线 与双曲线
与双曲线 ,且线段
,且线段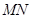 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为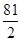 ,求
,求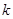 的取值范围。
的取值范围。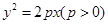 的焦点为
的焦点为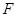 ,其准线与
,其准线与 轴的交点为
轴的交点为 ,过
,过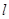 交抛物线于
交抛物线于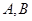 两点.
两点.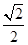 ,求证:
,求证: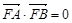 ;
;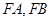 的斜率分别为
的斜率分别为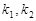 ,求
,求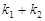 的值.
的值.