题目内容
已知曲线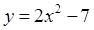 ,求曲线过点
,求曲线过点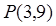 的切线方程。
的切线方程。

解析试题分析:因为点 不在曲线上,故先设所求切线的切点为
不在曲线上,故先设所求切线的切点为 ,再求
,再求 的导数
的导数 则
则 ,由点斜式写出所求切线方程
,由点斜式写出所求切线方程 ,再将切线上的已知点
,再将切线上的已知点 代入切线方程可求出
代入切线方程可求出 ,从而所求出切线方程.
,从而所求出切线方程.
试题解析:  ,点
,点 不在曲线上,设所求切线的切点为
不在曲线上,设所求切线的切点为 ,则切线的斜率
,则切线的斜率 ,
,
故所求的切线方程为 .
.
将 及
及 代入上式得
代入上式得
解得: 所以切点为
所以切点为 或
或 .
.
从而所求切线方程为
考点:1、过曲线外一点求曲线的切线方程;2、导数的几何意义.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 ,且经过点
,且经过点 ,直线
,直线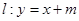 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B. 不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
不过点M,求证:直线MA、MB与x轴围成一个等腰三角形 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为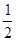
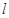 经过点
经过点 (0,1),且与椭圆C交于
(0,1),且与椭圆C交于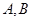 两点,若
两点,若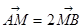 ,求直线
,求直线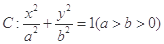 的离心率为
的离心率为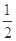 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线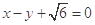 相切,过点P(4,0)且不垂直于x轴直线
相切,过点P(4,0)且不垂直于x轴直线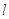 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.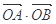 的取值范围;
的取值范围;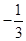 .
. :
: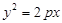 和⊙
和⊙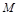 :
: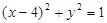 ,过抛物线
,过抛物线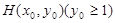 作两条直线与⊙
作两条直线与⊙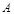 、
、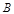 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点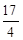 .
.
 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线 的斜率;
的斜率;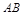 在
在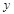 轴上的截距为
轴上的截距为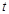 ,求
,求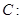
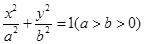 的离心率为
的离心率为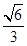 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为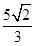 .
. 的方程;
的方程;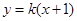 与椭圆
与椭圆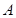 、
、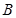 两点. ①若线段
两点. ①若线段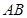 中点的横坐标为
中点的横坐标为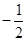 ,求斜率
,求斜率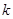 的值;②若点
的值;②若点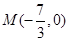 ,求证:
,求证: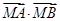 为定值.
为定值.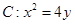 的焦点为
的焦点为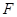 ,过点
,过点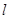 交抛物线
交抛物线 于
于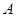 、
、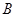 两点,经过
两点,经过 、
、 ,切线
,切线 .
.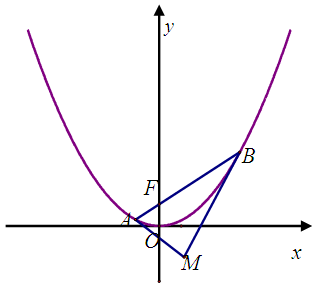
 在第二象限,且到准线距离为
在第二象限,且到准线距离为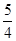 时,求
时,求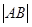 ;
;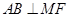 .
.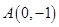 ,焦点在
,焦点在 轴上,若右焦点到直线
轴上,若右焦点到直线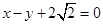 的距离为3.
的距离为3.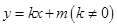 与椭圆相交于不同的两点
与椭圆相交于不同的两点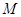 、
、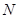 ,当
,当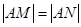 时,求
时,求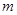 的取值范围.
的取值范围.