题目内容
(本题满分14分)
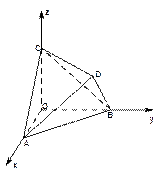
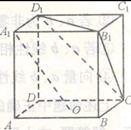
已知四边形ABCD是正方形,P是平面ABCD外一点,且PA=PB=PC=PD=AB=2,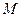 是棱
是棱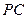 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
(1)求证: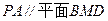 ;
;
(2) 求证: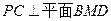 ;
;
(3)求直线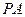 与直线
与直线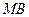 所成角的余弦值.
所成角的余弦值.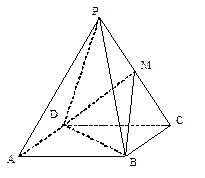
已知四边形ABCD是正方形,P是平面ABCD外一点,且PA=PB=PC=PD=AB=2,
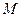 是棱
是棱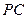 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:(1)求证:
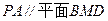 ;
;(2) 求证:
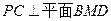 ;
;(3)求直线
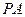 与直线
与直线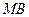 所成角的余弦值.
所成角的余弦值.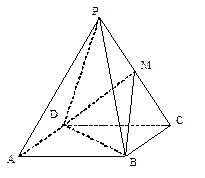
解:连结AC、BD交于点O,连结OP。

∵四边形ABCD是正方形, ∴AC⊥BD
∴AC⊥BD
∵PA=PC,∴OP⊥AC,同理OP⊥BD,
以O为原点,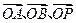 分别为
分别为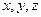 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系 …2分
…2分
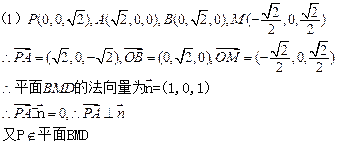
 …………………6分
…………………6分
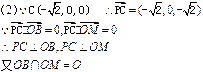
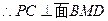 …………………10分
…………………10分
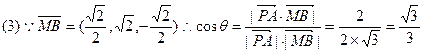
 …………………14分
…………………14分

∵四边形ABCD是正方形,
 ∴AC⊥BD
∴AC⊥BD∵PA=PC,∴OP⊥AC,同理OP⊥BD,
以O为原点,
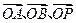 分别为
分别为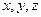 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系 …2分
…2分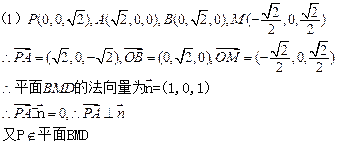
 …………………6分
…………………6分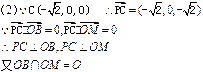
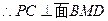 …………………10分
…………………10分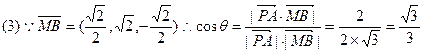
 …………………14分
…………………14分略

练习册系列答案
相关题目
 为正三角形,
为正三角形, 平面
平面 ,
, 是
是 的中点,
的中点,
 平面
平面 。
。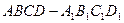 中,
中,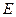 、
、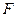 分别为棱
分别为棱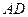 、
、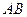 的中点.
的中点.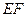 ∥平面
∥平面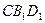 ;
;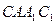 ⊥平面
⊥平面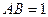 ,一个动点从点
,一个动点从点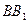 、
、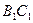 、
、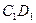 、
、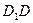 、
、 上的点,最终又回到点
上的点,最终又回到点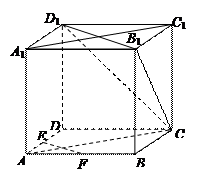
 ,D为B1C1的中点。
,D为B1C1的中点。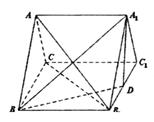
 (12分)
(12分)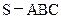 中,△ABC是边长为4的正三角形,平面
中,△ABC是边长为4的正三角形,平面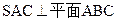 ,
, ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。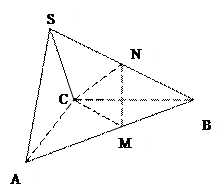
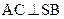 ;
;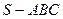 中,
中,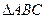
 是边长为
是边长为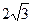 的正三角形,平面
的正三角形,平面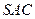 ⊥平面
⊥平面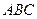 ,
,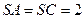 ,
,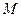 、
、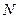 分别为
分别为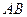 、
、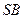 的中点。
的中点。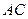 ⊥
⊥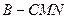 的体积.
的体积.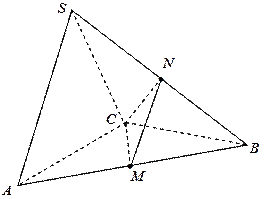
 平面AB1C1
平面AB1C1 的顶点
的顶点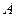 、
、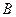 、
、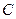 分别在两两垂直的三条射线
分别在两两垂直的三条射线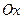 、
、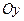 、
、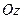 上,给出下列四个命题:
上,给出下列四个命题: 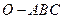 是正三棱锥;
是正三棱锥;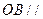 平面
平面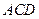 ;
;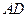 与
与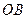 所成的角为
所成的角为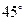 ;
; 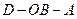 为
为