题目内容
(本小题满分14分)
在三棱锥
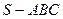 中,
中,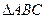
 是边长为
是边长为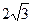 的正三角形,平面
的正三角形,平面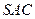 ⊥平面
⊥平面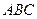 ,
,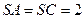 ,
,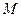 、
、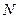 分别为
分别为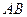 、
、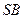 的中点。
的中点。(1)证明:
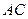 ⊥
⊥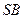 ;
;(2)求三棱锥
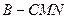 的体积.
的体积.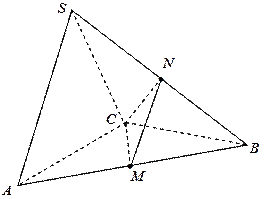
(1)略
(2)

证明:(1)如图,取
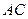 中点
中点 ,连结
,连结 ,
, .………1分
.………1分∵
 ,
, ∴
 . ………………………3分
. ………………………3分又∵
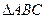 是正三角形,
是正三角形, ∴
 . …………………………5分
. …………………………5分 ∵
 ,
,∴
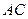 ⊥平面
⊥平面 . ……………………
. …………………… ……6分
……6分又∵
 平面
平面 ,
,∴
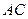 ⊥
⊥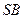 . …………………………7分
. …………………………7分 解:(2)∵
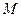 是
是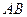 的中点,
的中点,∴
 . ……………………………9分
. ……………………………9分∵平面
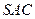 ⊥平面
⊥平面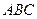 ,
, ,
, ∴
 平面
平面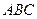 . …………………………10分
. …………………………10分又∵
 ,
, ,
, ∴
 ,即点
,即点 到平面
到平面 的距离为1.
的距离为1.∵
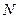 是
是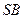 的中点,
的中点, ∴点
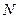 到平面
到平面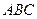 的距离为
的距离为 . ………………………………12分
. ………………………………12分∴
 ………………………………14分
………………………………14分
练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
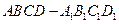 中,
中,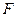 为
为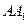 的中点,求证:
的中点,求证: 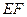 ∥面
∥面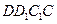 ;
;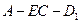 的余弦值;
的余弦值;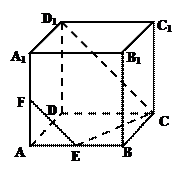
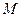 是棱
是棱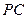 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: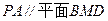 ;
;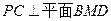 ;
;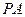 与直线
与直线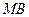 所成角的余弦值.
所成角的余弦值.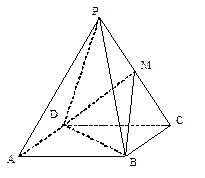

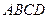 中,
中,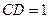 ,
,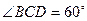 ,且
,且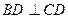 ,正方形
,正方形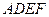 所在平面和平面
所在平面和平面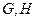 分别是
分别是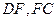 的中点.
的中点.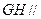 平面
平面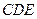 ;
;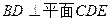 ;
;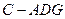 的体积.
的体积.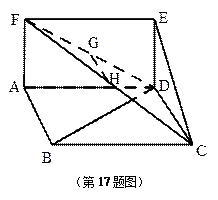
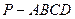 中,底面
中,底面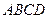 是直角梯形,
是直角梯形,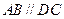 ,
,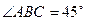 ,
,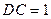 ,
,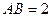 ,
,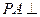 平面
平面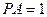 .
. 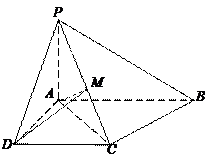
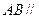 平面
平面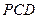 ;
;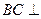 平面
平面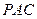 ;
; 的正方体ABCD-A1B1C1D1中
的正方体ABCD-A1B1C1D1中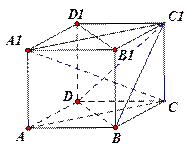
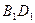 ∥平面C1BD
∥平面C1BD 平面C1BD
平面C1BD