题目内容
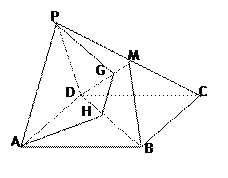
.(本小题满分12分)如图,在正方体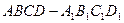 中,
中,
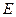 、
、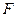 分别为棱
分别为棱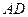 、
、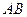 的中点.
的中点.
(1)求证: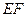 ∥平面
∥平面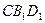 ;
;
(2)求证:平面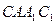 ⊥平面
⊥平面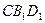 ;
;
(3)如果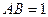 ,一个动点从点
,一个动点从点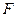 出发在正方体的
出发在正方体的
表面上依次经过棱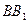 、
、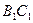 、
、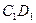 、
、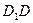 、
、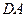 上的点,最终又回到点
上的点,最终又回到点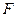 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
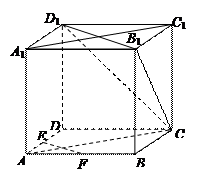
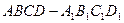 中,
中,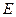 、
、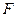 分别为棱
分别为棱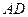 、
、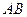 的中点.
的中点.(1)求证:
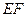 ∥平面
∥平面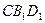 ;
;(2)求证:平面
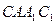 ⊥平面
⊥平面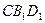 ;
;(3)如果
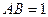 ,一个动点从点
,一个动点从点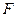 出发在正方体的
出发在正方体的表面上依次经过棱
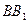 、
、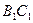 、
、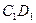 、
、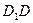 、
、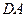 上的点,最终又回到点
上的点,最终又回到点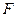 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
(1)证明:连结 .
.
在正方体 中,对角线
中,对角线 .
.
又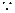 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
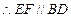 .
.
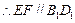 . …………2分
. …………2分
又B1D1平面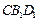 ,
,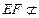 平面
平面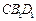 ,
,
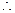 EF∥平面CB1D1. …………4分
EF∥平面CB1D1. …………4分
(2)证明: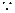 在正方体
在正方体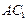 中,AA1⊥平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,
而B1D1平面A1B1C1D1,
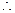 AA1⊥B1D1.
AA1⊥B1D1.
又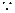 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,
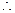 B1D1⊥平面CAA1C1. …………6分
B1D1⊥平面CAA1C1. …………6分
又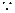 B1D1平面CB1D1,
B1D1平面CB1D1,
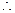 平面CAA1C1⊥平面CB1D1. …………8分
平面CAA1C1⊥平面CB1D1. …………8分
(3)最小值为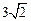 . …………9分
. …………9分
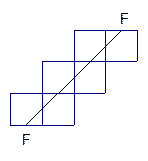
如图,将正方体六个面展开成平面图形, …………10分
从图中F到F,两点之间线段最短,而且依次经过棱BB1、B1C1、C1D1、D1D、DA上的中点,所求的最小值为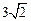 . …………12分.
. …………12分.
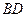 .
.
在正方体
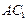 中,对角线
中,对角线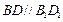 .
.又
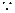 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,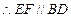 .
.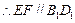 . …………2分
. …………2分又B1D1平面
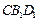 ,
,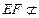 平面
平面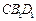 ,
,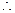 EF∥平面CB1D1. …………4分
EF∥平面CB1D1. …………4分(2)证明:
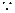 在正方体
在正方体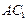 中,AA1⊥平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
 AA1⊥B1D1.
AA1⊥B1D1.又
 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1, B1D1⊥平面CAA1C1. …………6分
B1D1⊥平面CAA1C1. …………6分又
 B1D1平面CB1D1,
B1D1平面CB1D1,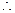 平面CAA1C1⊥平面CB1D1. …………8分
平面CAA1C1⊥平面CB1D1. …………8分(3)最小值为
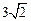 . …………9分
. …………9分如图,将正方体六个面展开成平面图形, …………10分
从图中F到F,两点之间线段最短,而且依次经过棱BB1、B1C1、C1D1、D1D、DA上的中点,所求的最小值为
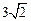 . …………12分.
. …………12分.略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
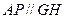
 中,
中, ∥
∥ ,
,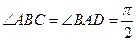 ,
,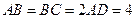 ,
,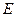 、
、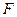 分别是
分别是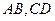 上的点,
上的点,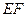 ∥
∥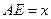 ,
,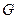 是
是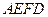 ⊥平面
⊥平面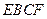 (如图) .
(如图) .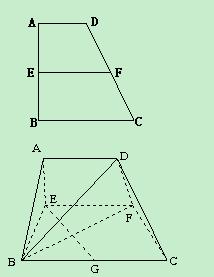
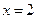 时,求证:
时,求证: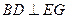 ;
; 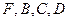 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为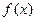 ,求
,求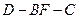 的余弦值.
的余弦值.
 ,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.
,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点. D所成角的正弦值;
D所成角的正弦值; 的体积为
的体积为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。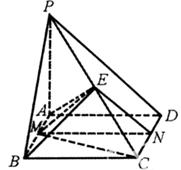
 是棱
是棱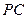 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: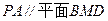 ;
;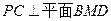 ;
;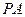 与直线
与直线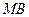 所成角的余弦值.
所成角的余弦值.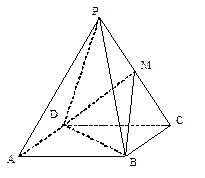
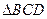 中,
中,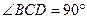 ,
,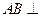 平面
平面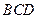 ,
,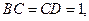
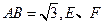 分别为
分别为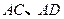 的中点.
的中点.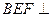 平面
平面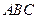 ;
;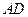 与平面
与平面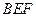 所成角的正弦值.
所成角的正弦值.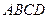 中,
中,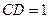 ,
,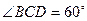 ,且
,且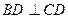 ,正方形
,正方形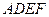 所在平面和平面
所在平面和平面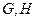 分别是
分别是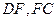 的中点.
的中点.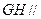 平面
平面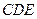 ;
; ;
; 的体积.
的体积.
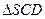 内及其边界上运动,并且总是保持PE
内及其边界上运动,并且总是保持PE AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是( ).
AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是( ).