题目内容
已知椭圆的参数方程
（θ为参数），求椭圆上的动点P到直线
（t为参数）的最短距离．
解：直线（t为参数） 即 2x+3y-10=0．椭圆 即 
+
=1．
设椭圆上的动点P（3cosθ，2sinθ）到直线的距离等于
d=
=
，
∵6
sin（θ+
）-10∈[-6-10，6-10]，∴∈[
，
]，
∴d的最小值为．
分析：设动点P（3cosθ，2sinθ），由点到直线的距离公式求出它到直线的距离d，再由及正弦函数的有界性求出答案．
点评：本题考查点到直线的距离公式的应用，椭圆的参数方程，以及正弦函数的有界性．利用正弦函数的有界性求出d的最小值是本题的难点，属于中档题．
（t为参数） 即 2x+3y-10=0．椭圆 即 +=1．设椭圆上的动点P（3cosθ，2sinθ）到直线的距离等于
d=
=，∵6
sin（θ+ ）-10∈[-6-10，6-10]，∴∈[，]，∴d的最小值为
．分析：设动点P（3cosθ，2sinθ），由点到直线的距离公式求出它到直线的距离d，再由及正弦函数的有界性求出答案．
点评：本题考查点到直线的距离公式的应用，椭圆的参数方程，以及正弦函数的有界性．利用正弦函数的有界性求出d的最小值是本题的难点，属于中档题．
练习册系列答案
相关题目
，点M在椭圆上，点O为原点，则当
时，OM的斜率为（ ）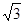
D．
（
为参数），求椭圆上的动点P到直线
（t为参数）的最短距离。