题目内容
已知椭圆的参数方程为
(?为参数)，点M在椭圆上，点O为原点，则当?=
时，OM的斜率为（ ）
|
| π |
| 3 |
分析：将点对应的参数代入椭圆的参数方程得到M的坐标，再利用直线的斜率公式即可求出答案．
解答：解：当?=
时，点M的坐标为（cos
，2sin
），即M（
，
），
∴OM的斜率为k=
=2
．
故选D．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
∴OM的斜率为k=
| ||
|
| 3 |
故选D．
点评：本题主要考查了椭圆的参数方程，直线的斜率等基本知识，属于基础题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
，点M在椭圆上，点O为原点，则当
时，OM的斜率为（ ）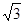
D．
（
），则该椭圆的焦距为
. 
（θ∈R），则该椭圆的焦距为 ．