题目内容
a、b、c、d∈R,且ad-bc=1，求证：a2+b2+c2+d2+ab+cd≠1.
证明：假设a2+b2+c2+d2+ab+cd=1,则有a2+b2+c2+d2+ab+cd-ad+bc=0
(a+b)2+(a-d)2+(b+c)2+(d+c)2=0.
由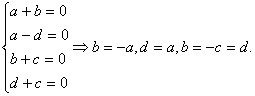
有-a=a,即a=0.
∴ad-bc=a2-(-a·a)=0.
这与ad-bc=1矛盾，∴假设a2+b2+c2+d2+ab+cd=1不成立，故a2+b2+c2+d2+ab+cd≠1.
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
设a、b、c、d∈R，若
为实数，则（ ）
| a+bi |
| c+di |
| A、bc+ad≠0 |
| B、bc-ad≠0 |
| C、bc-ad=0 |
| D、bc+ad=0 |
设a，b，c，d∈R，则条件甲：ac=2（b+d）是条件乙：方程x2+ax+b=0与方程x2+cx+d=0中至少有一个有实根的（ ）
| A、充分而不必要条件 | B、必要而不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
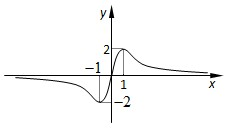若函数f（x）=