题目内容

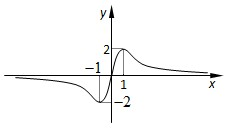若函数f（x）=
bx+cx2+ax+1
（a，b，c∈R）（a，b，c，d∈R），其图象如图所示，则a+b+c=
4
4
．
分析：将（-1，-2），（0，0），（1，2）代入函数关系式f（x）=
bx+c
x2+ax+1
，从而可建立方程组，可求 a=0，b=4，c=0
故可求a+b+c的值．
解答：解：根据图象，将（-1，-2），（0，0），（1，2）代入函数关系式得
-b+c
2-a
=-2
c=0
b+c
2+a
=2
，解得a=0，b=4，c=0
∴a+b+c=4
故答案为4．
点评：本题以函数图象为载体，考查函数的解析式，体现了数形结合的数学思想．
练习册系列答案
相关题目
已知以下四个命题：
①如果x1，x2是一元二次方程ax2+bx+c=0的两个实根，且x1＜x2，那么不等式ax2+bx+c＜0的解集为{x|x1＜x＜x2}．
②若
x-1x-2
≤0，则（x-1）（x-2）≤0．
③“若M={-1，0，1}，则x2-2x+m＞0的解集是实数集R”的逆否命题．
④若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
其中为真命题的是
 
（填上你认为正确的序号）．
14、若函数f（x）=（x+a）（bx+a）（常数a，b∈R）是偶函数，且它的值域为（-∞，4]，则该函数的解析式为f（x）=
-x2+4
．
（2007•揭阳二模）如图（1）示，定义在D上的函数f（x），如果满足：对?x∈D，?常数A，都有f（x）≥A成立，则称函数f（x）在D上有下界，其中A称为函数的下界．（提示：图（1）、（2）中的常数A、B可以是正数，也可以是负数或零）  

（Ⅰ）试判断函数f（x）=x3+
48
x
在（0，+∞）上是否有下界？并说明理由；
（Ⅱ）又如具有如图（2）特征的函数称为在D上有上界．请你类比函数有下界的定义，给出函数f（x）在D上有上界的定义，并判断（Ⅰ）中的函数在（-∞，0）上是否有上界？并说明理由；
（Ⅲ）若函数f（x）在D上既有上界又有下界，则称函数f（x）在D上有界，函数f（x）叫做有界函数．试探究函数f（x）=ax3+
b
x
（a＞0，b＞0a，b是常数）是否是[m，n]（m＞0，n＞0，m、n是常数）上的有界函数？
已知函数f（x）=
1
3
x3-bx+c（b，c∈R）
（Ⅰ）若函数f（x）在点（1，f（1））处的切线方程为y=2x+1，求b，c的值；
（Ⅱ）若b=1，函数f（x）在区间（0，2）内有唯一零点，求c的取值范围；
（Ⅲ）若对任意的x1，x2∈[-1，1]，均有|f（x1）-f（x2）|≤
4
3
，求b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网