题目内容
将一块圆心角为![]() ,半径为
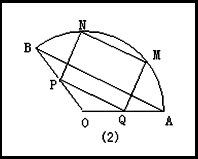
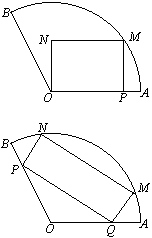
,半径为![]() ㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.
㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.

最大面积为![]()
![]()
解析:
按图(1)的裁法:矩形的一边OP在OA上,顶点M在圆弧上,设![]() ,则
,则
![]() ,所以矩形OPMN的面积
,所以矩形OPMN的面积![]()
即当![]() 时,
时,![]() .
.
按图(2)的裁法:矩形一边PQ与弦AB平行,设![]() ,在△MOQ中,
,在△MOQ中,
![]() ,则正弦定理得:
,则正弦定理得:![]()
又![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]()
由于![]() ,所以用第二种裁法得面积最大的矩形,最大面积为
,所以用第二种裁法得面积最大的矩形,最大面积为![]()
![]() .
.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
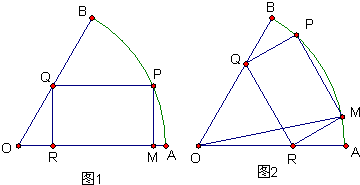
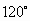 ,半径为20cm的扇形铁片裁成一块矩形,如下图所示有两种裁法:(让矩形一边在扇形的一条半径OA上,如图(1);或让矩形一边与扇形的弦AB平行,如图(2),请问哪一种裁法能得到最大面积的矩形?并求出这个最大值.
,半径为20cm的扇形铁片裁成一块矩形,如下图所示有两种裁法:(让矩形一边在扇形的一条半径OA上,如图(1);或让矩形一边与扇形的弦AB平行,如图(2),请问哪一种裁法能得到最大面积的矩形?并求出这个最大值.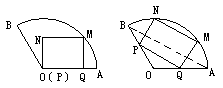
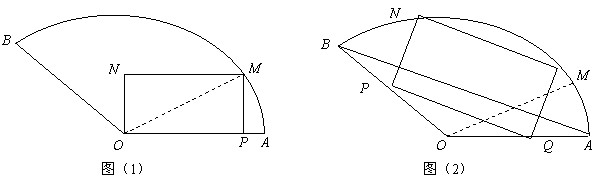 就可以得出问题的结论.
就可以得出问题的结论.