题目内容
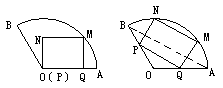
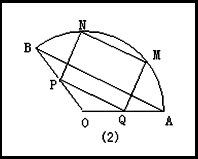
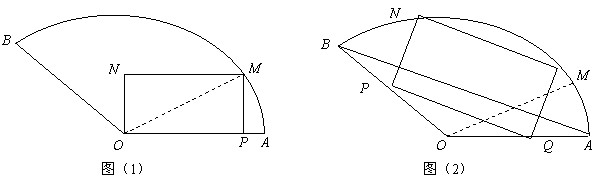
将一块圆心角为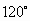
，半径为20cm的扇形铁片裁成一块矩形，如下图所示有两种裁法：(让矩形一边在扇形的一条半径OA上，如图(1)；或让矩形一边与扇形的弦AB平行，如图(2)，请问哪一种裁法能得到最大面积的矩形？并求出这个最大值．
答案：
解析：
解析：
|
解：在图(1)中，连结OM，设∠AOM＝θ( 在图(2)中，过O作OD⊥AB，分别交PQ、MN于E、F，则∠AOD＝ 在△OMQ中，由正弦定理，得 ∴|MQ|＝ ∴矩形PQMN的面积为 ∴当 ∵ |
＜θ＜
)则矩形PQMN的面积为
＝|PQ|·|QM|＝
sinθcosθ＝200
，设∠AOM＝
(
＝|MN|·|MQ|＝
，即
时，
有最大值为
＞200，∴第二种裁法能得到最大面积是
练习册系列答案
相关题目
，半径为
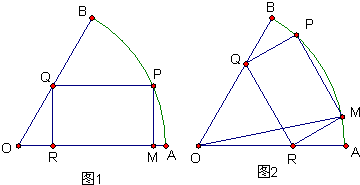
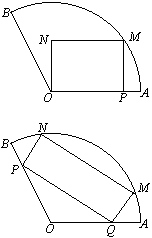
㎝的扇形铁片裁成一块矩形，有如图(1)、(2)的两种裁法：让矩形一边在扇形的一条半径OA上，或让矩形一边与弦AB平行，请问哪 种裁法能得到最大面积的矩形？并求出这个最大值.
，半径为20厘米的扇形铁片裁成一块矩形，请你设计裁法，使裁得矩形的面积最大?并说明理由．
上，或让矩形一边与弦
平行。从图形的特点来看，涉及到线段的长度和角度，将这些量放置在三角形中，通过解三角形求出矩形的边长，再计算出两种方案所得矩形的最大面积，加以比较，
就可以得出问题的结论．