题目内容
8.已知(2x2-x+1)(1-2x)6=a0+a1x+a2x2+…+a8x8.(1)求a2;
(2)求(a2+a4+a6+a8)2-(a1+a3+a5+a7)2.
分析 (1)利用展开式的通项公式,求得a2的值.
(2)令x=0,可得a0 =1,再分别令x=1、x=-1,可得两个式子,化简这2个式子,可得要求式子的值.
解答 解:(1)分析项的构成,知:${a_2}=2•1+({-1})•({-2C_6^1})+1•({4C_6^2})=74$.
(2)原式=(a1+a2+a3+…+a8)(-a1+a2-a3+a4-a5+a6-a7+a8),
令x=0,得a0=1,
令x=1,得a0+a1+a2+a3+…+a8=2⇒a1+a2+a3+…+a8=1,
令x=-1,得a0-a1+a2-a3+a4-a5+a6-a7+a8=2916⇒-a1+a2-a3+a4-a5+a6-a7+a8=2915
从而原式=2915.
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题

练习册系列答案
相关题目
16.|$\overrightarrow{a}$|=2,向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为120°,则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$方向上的投影等于( )
| A. | 2 | B. | 1 | ||
| C. | -1 | D. | 由向量 b 的长度确定 |
13.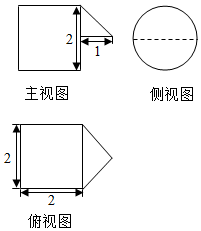 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{1}{3}+2π$ | B. | $\frac{13}{6}π$ | C. | $\frac{7π}{3}$ | D. | $\frac{5π}{2}$ |
3.已知椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1的左、右焦点分别为F1,F2,过F1且倾斜角为45°的直线l与椭圆相交于A,B两点.则AB的中点坐标( )
| A. | (-$\frac{3}{5}$,$\frac{2}{5}$) | B. | (1,-1) | C. | (-1,$\frac{2}{5}$) | D. | (-1,1) |
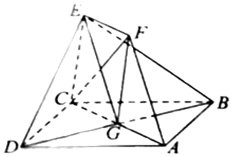 (理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.