题目内容
如图(5)所示,已知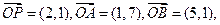 设
设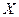 是直线
是直线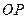 上的一点, (其中
上的一点, (其中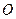 为坐标原点).
为坐标原点).
(Ⅰ)求使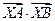 取最小值时的点
取最小值时的点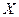 的坐标和此时
的坐标和此时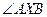 的余弦值.
的余弦值.
(Ⅱ)对于(Ⅰ)中的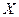 .若
.若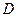 是线段
是线段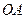 的三等分点,且
的三等分点,且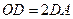 ,
,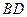 与
与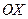 交于点
交于点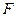 ,设
,设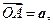
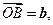 试用
试用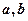 表示
表示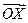 和
和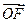 .
.

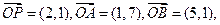 设
设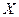 是直线
是直线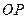 上的一点, (其中
上的一点, (其中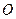 为坐标原点).
为坐标原点).(Ⅰ)求使
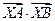 取最小值时的点
取最小值时的点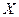 的坐标和此时
的坐标和此时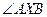 的余弦值.
的余弦值. (Ⅱ)对于(Ⅰ)中的
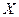 .若
.若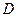 是线段
是线段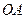 的三等分点,且
的三等分点,且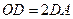 ,
,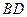 与
与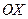 交于点
交于点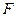 ,设
,设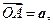
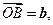 试用
试用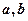 表示
表示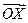 和
和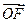 .
. 
(Ⅰ)
 (Ⅱ)
(Ⅱ) 


(Ⅰ)因为
 三点共线,所以
三点共线,所以 -----1分
-----1分 --------2分
--------2分 --------4分
--------4分所以当
 即
即 时,
时, 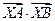 取最小值--------5分
取最小值--------5分此时

 ----------7分
----------7分(Ⅱ) 因为
 ,令存在实数
,令存在实数 ,使得
,使得
 ----9分
----9分因为
 ,由B,F,D三点共线,可知存在实数
,由B,F,D三点共线,可知存在实数 使得
使得


--11分
又因为O,F,X三点共线,所以存在实数
 使得,
使得, ---------------13分
---------------13分所以
 ------14分
------14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
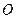 为坐标原点,
为坐标原点,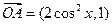 ,
,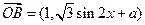 (
(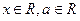 ,
,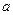 是常数),若
是常数),若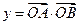
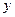 关于
关于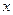 的函数关系式
的函数关系式 ;
; 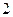 ,求
,求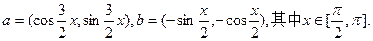
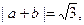 求x的值;
求x的值;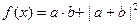 ,若
,若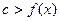 恒成立,求实数c的取值范围。
恒成立,求实数c的取值范围。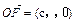 (c>0),
(c>0),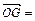 (n, n)(n∈R),
(n, n)(n∈R), 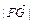 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:①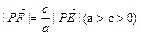 ,②
,②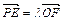 (其中
(其中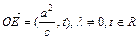 );③动点P的轨迹C经过点B(0,-1)。
);③动点P的轨迹C经过点B(0,-1)。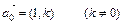 的直线l与曲线C交于不同两点M、N,若
的直线l与曲线C交于不同两点M、N,若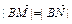 ,求k的取值范围。
,求k的取值范围。
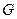








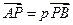
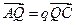

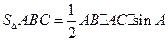 )
) ;(2)求
;(2)求 的取值范围
的取值范围 ,
,
 且
且 ,求向量
,求向量 ;
; 与向量
与向量 共线,当
共线,当 时,且
时,且 取最大值为4时,求
取最大值为4时,求
 ,
, ,
, 且
且 ,
, ,求点
,求点 ,
, 及向量
及向量 的坐标.
的坐标.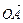 、
、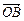 、
、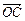 ,其中与
,其中与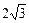 ,若
,若