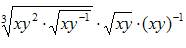题目内容
已知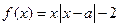 .
.
(I)当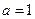 时,解不等式
时,解不等式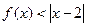 ;
;
(II)当 时,
时,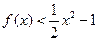 恒成立,求实数
恒成立,求实数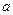 的取值范围.
的取值范围.
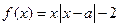 .
.(I)当
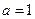 时,解不等式
时,解不等式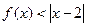 ;
;(II)当
 时,
时,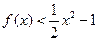 恒成立,求实数
恒成立,求实数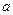 的取值范围.
的取值范围. (1)不等式的解集为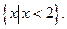 (2)
(2)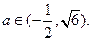
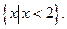 (2)
(2)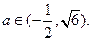
(I)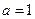 时,
时,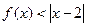 ,即
,即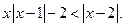 (※)
(※)
(1)当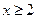 时,由(※)
时,由(※)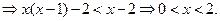
又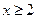 ,
,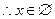
(2)当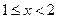 时,由(※)
时,由(※)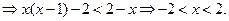
又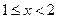 ,
,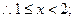
(3)当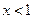 时,由(※)
时,由(※)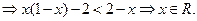
又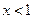 ,
,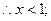
综上:由(1)、(2)、(3)知原不等式的解集为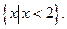
(II)当 时,
时,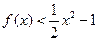 ,即
,即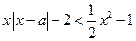 恒成立,
恒成立,
也即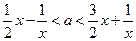 在
在 上恒成立。
上恒成立。
而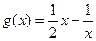 在
在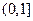 上为增函数,故
上为增函数,故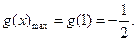
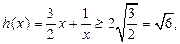 当且仅当
当且仅当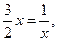 即
即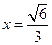 时,等号成立.
时,等号成立.
故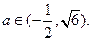
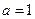 时,
时,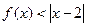 ,即
,即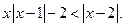 (※)
(※)(1)当
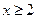 时,由(※)
时,由(※)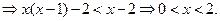
又
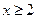 ,
,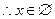
(2)当
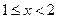 时,由(※)
时,由(※)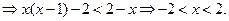
又
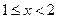 ,
,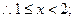
(3)当
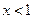 时,由(※)
时,由(※)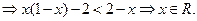
又
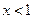 ,
,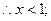
综上:由(1)、(2)、(3)知原不等式的解集为
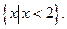
(II)当
 时,
时,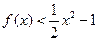 ,即
,即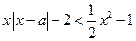 恒成立,
恒成立,也即
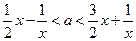 在
在 上恒成立。
上恒成立。而
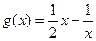 在
在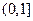 上为增函数,故
上为增函数,故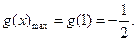
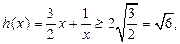 当且仅当
当且仅当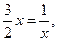 即
即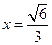 时,等号成立.
时,等号成立.故
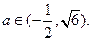

练习册系列答案
相关题目
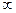 )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有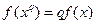 .
.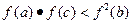 ;
;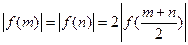 ,求证:
,求证: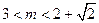
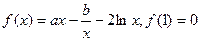 ,
,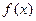 在其定义域内为单调函数,求
在其定义域内为单调函数,求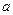 的取值范围;
的取值范围;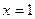 处的切线的斜率为0,且
处的切线的斜率为0,且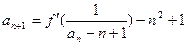 , 已知
, 已知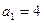 ,求证:
,求证: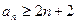
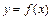 是定义在区间
是定义在区间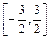 上的偶函数,且
上的偶函数,且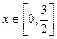 时,
时,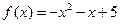 (1).求函数
(1).求函数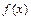 的解析式;(2).若矩形
的解析式;(2).若矩形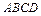 的顶点
的顶点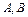 在函数
在函数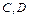 在
在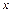 轴上,求矩形
轴上,求矩形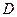 上的函数
上的函数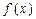 ,如果满足:对任意
,如果满足:对任意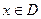 ,存在常数
,存在常数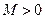 ,都有
,都有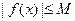 成立,则称
成立,则称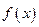 是
是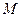 称为函数
称为函数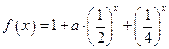 .
. 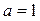 时,求函数
时,求函数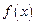 在
在 上的值域,并判断函数
上的值域,并判断函数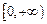 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数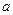 的取值范围.
的取值范围.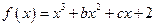 在
在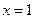 处取得极值
处取得极值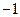 .
.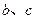 的值;
的值; 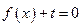 在区间
在区间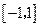 上有实根,求实数的取值范围.
上有实根,求实数的取值范围.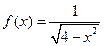 的定义域是A, 函数
的定义域是A, 函数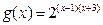
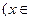 定义域B
定义域B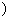 的值域是
的值域是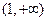 .
. 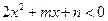 的解集是A,求
的解集是A,求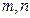 的值.
的值. 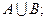
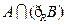 (R是实数集).
(R是实数集).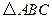 中,
中, ,
,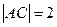 ,
,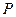 、
、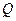 分别是
分别是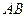 、
、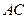 上的动点,且满足
上的动点,且满足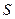
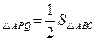 ,若
,若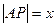 ,
,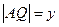 ,
,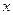 的取值范围,
的取值范围,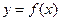 的解析式.
的解析式.