题目内容
定义在区间(0,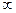 )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有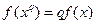 .
.
(1)求证:方程f(x)=0有且只有一个实根;
(2)若a>b>c>1,且a、b、c成等差数列,求证: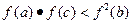 ;
;
(3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有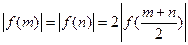 ,求证:
,求证: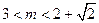
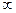 )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有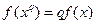 .
.(1)求证:方程f(x)=0有且只有一个实根;
(2)若a>b>c>1,且a、b、c成等差数列,求证:
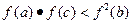 ;
;(3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有
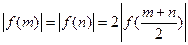 ,求证:
,求证: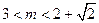
证明见解析
(1)取x=1,q=2,有
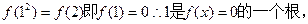 若存在另一个实根
若存在另一个实根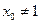 ,使得
,使得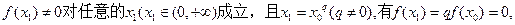
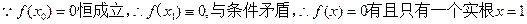
(2)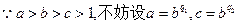 ,
,
,则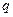
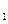
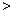 0,
0,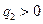 ∴
∴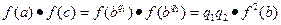 ,又a+c=2b,
,又a+c=2b,
∴ac-b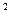 =
=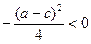
即ac<b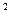
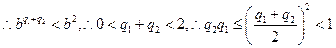
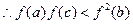
(3)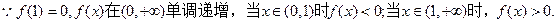
又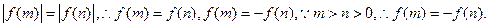
令m=b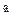 ,n=
,n=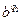 ,b
,b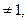 且q
且q
则f(m)+f(n)=(q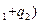 f(b)=f(mn)=0
f(b)=f(mn)=0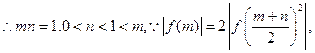 且
且
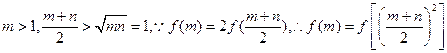
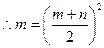
即4m=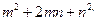
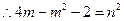 ,由0<n<1得
,由0<n<1得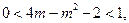
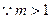 ,
,
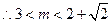
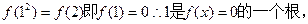 若存在另一个实根
若存在另一个实根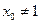 ,使得
,使得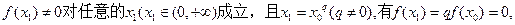
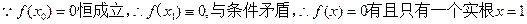
(2)
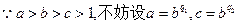 ,
,,则
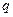
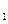
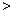 0,
0,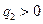 ∴
∴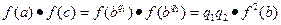 ,又a+c=2b,
,又a+c=2b,∴ac-b
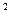 =
=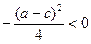
即ac<b
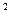
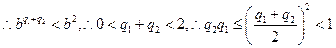
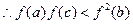
(3)
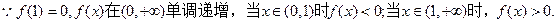
又
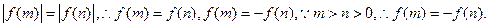
令m=b
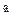 ,n=
,n=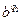 ,b
,b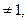 且q
且q
则f(m)+f(n)=(q
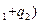 f(b)=f(mn)=0
f(b)=f(mn)=0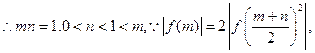 且
且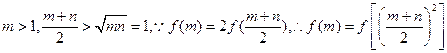
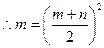
即4m=
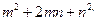
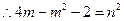 ,由0<n<1得
,由0<n<1得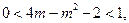
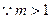 ,
,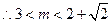

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
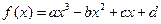 (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值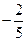 .
.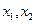 ∈[-1,1],不等式
∈[-1,1],不等式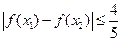 成立;
成立;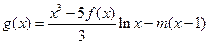 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.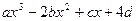 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值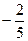 。
。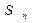 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f (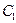 )-f(
)-f( )|≤
)|≤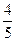 。
。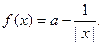
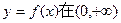 上是增函数.
上是增函数. 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.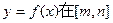 上的值域是
上的值域是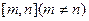 ,求实数a的取值范围.
,求实数a的取值范围. +lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,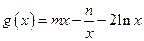 .
.  恒成立;
恒成立;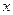 的方程:
的方程: 根的个数.
根的个数.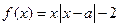 .
.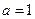 时,解不等式
时,解不等式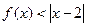 ;
; 时,
时,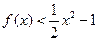 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.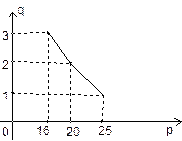
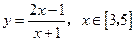 的最小值和最大值.
的最小值和最大值.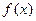 是
是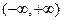 上的偶函数,若对于
上的偶函数,若对于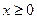 ,都有
,都有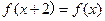 ,且当
,且当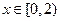 时,
时,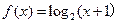 ,则
,则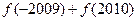 的值为 ( )
的值为 ( )