题目内容
已知函数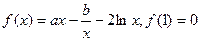 ,
,
(1)若函数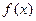 在其定义域内为单调函数,求
在其定义域内为单调函数,求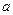 的取值范围;
的取值范围;
(2)若函数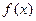 的图象在
的图象在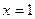 处的切线的斜率为0,且
处的切线的斜率为0,且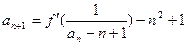 , 已知
, 已知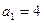 ,求证:
,求证: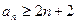
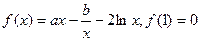 ,
,(1)若函数
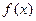 在其定义域内为单调函数,求
在其定义域内为单调函数,求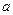 的取值范围;
的取值范围;(2)若函数
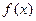 的图象在
的图象在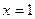 处的切线的斜率为0,且
处的切线的斜率为0,且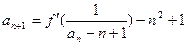 , 已知
, 已知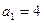 ,求证:
,求证: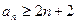
(1)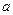 的取值范围为
的取值范围为 或
或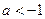 或
或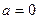 (2)同解析
(2)同解析
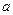 的取值范围为
的取值范围为 或
或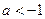 或
或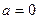 (2)同解析
(2)同解析(1)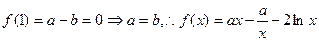
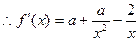
要使函数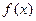 在定义域
在定义域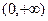 内为单调函数,则在
内为单调函数,则在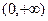 内
内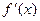 恒大于0或恒小于0,
恒大于0或恒小于0,
当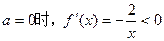 在
在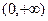 内恒成立;
内恒成立;
当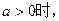 要使
要使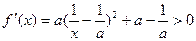 恒成立,则
恒成立,则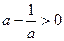 ,解得
,解得
当 要使
要使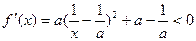 恒成立,则
恒成立,则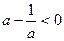 ,解得
,解得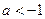
所以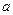 的取值范围为
的取值范围为 或
或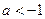 或
或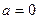
(2)根据题意得: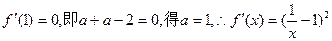
于是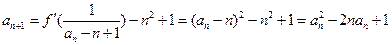
用数学归纳法证明如下:
当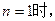
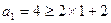 ,不等式成立;
,不等式成立;
假设当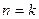 时,不等式
时,不等式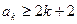 成立,即
成立,即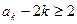 也成立,
也成立,
当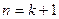 时,
时,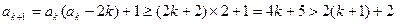
所以当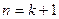 ,不等式也成立
,不等式也成立
综上得对所有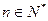 时,都有
时,都有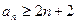
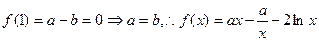
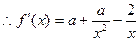
要使函数
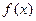 在定义域
在定义域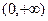 内为单调函数,则在
内为单调函数,则在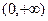 内
内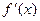 恒大于0或恒小于0,
恒大于0或恒小于0,当
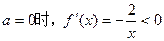 在
在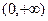 内恒成立;
内恒成立;当
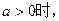 要使
要使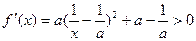 恒成立,则
恒成立,则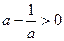 ,解得
,解得
当
 要使
要使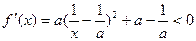 恒成立,则
恒成立,则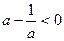 ,解得
,解得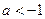
所以
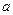 的取值范围为
的取值范围为 或
或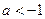 或
或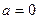
(2)根据题意得:
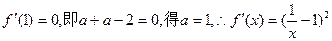
于是
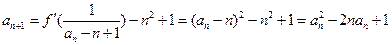
用数学归纳法证明如下:
当
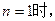
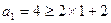 ,不等式成立;
,不等式成立;假设当
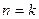 时,不等式
时,不等式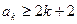 成立,即
成立,即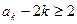 也成立,
也成立,当
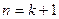 时,
时,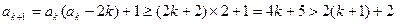
所以当
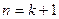 ,不等式也成立
,不等式也成立综上得对所有
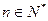 时,都有
时,都有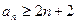

练习册系列答案
相关题目
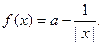
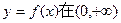 上是增函数.
上是增函数. 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.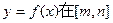 上的值域是
上的值域是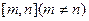 ,求实数a的取值范围.
,求实数a的取值范围.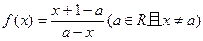
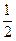 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];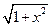 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.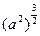 =a3 ②
=a3 ②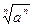 =|a| ③函数y=
=|a| ③函数y=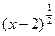 -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若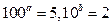 ,则2a+b=1
,则2a+b=1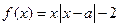 .
.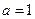 时,解不等式
时,解不等式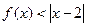 ;
; 时,
时,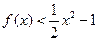 恒成立,求实数
恒成立,求实数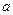 的取值范围.
的取值范围.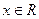 ,
,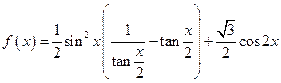 .
.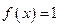 ,求
,求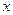 的值.
的值.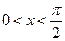 ,求
,求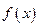 的单调的递减区间;
的单调的递减区间;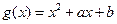 ,则
,则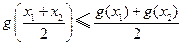 .
.