题目内容
已知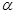 ,
,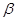 ,
,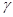 是三个互不重合的平面,
是三个互不重合的平面,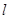 是一条直线,下列命题中正确命题是( )
是一条直线,下列命题中正确命题是( )
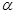 ,
,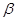 ,
,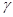 是三个互不重合的平面,
是三个互不重合的平面,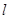 是一条直线,下列命题中正确命题是( )
是一条直线,下列命题中正确命题是( )A.若 , ,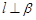 ,则 ,则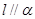 | B.若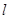 上有两个点到 上有两个点到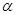 的距离相等,则 的距离相等,则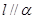 |
C.若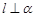 , ,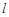 ∥ ∥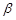 ,则 ,则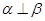 | D.若 , ,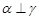 ,则 ,则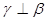 |
C
试题分析:A.若
 ,
,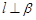 ,则
,则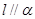 不对,有可能
不对,有可能 ;
;B.若
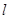 上有两个点到
上有两个点到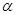 的距离相等,则
的距离相等,则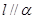 不对,有可能
不对,有可能 相交;
相交;C.若
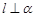 ,
,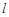 ∥
∥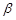 ,则
,则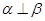 正确,经平移
正确,经平移 可以在平面
可以在平面 内,所以
内,所以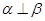 。
。点评:典型题,涉及立体几何的平行关系、垂直关系,是高考的必考内容,难度不大,要求定理、公理要记清。

练习册系列答案
相关题目
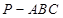 中,
中,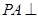 底面
底面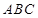 ,
,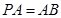 ,
,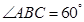 ,
,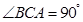 ,点
,点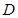 ,
,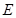 分别在棱
分别在棱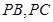 上,且
上,且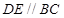
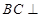 平面
平面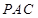 ;
;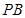 的中点时,求
的中点时,求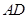 与平面
与平面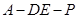 为直二面角?并说明理由.
为直二面角?并说明理由.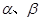 表示两个互相垂直的平面,
表示两个互相垂直的平面,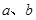 表示一对异面直线,则
表示一对异面直线,则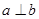 的一个充分条件是( )
的一个充分条件是( )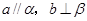 B.
B.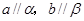
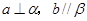 D.
D.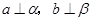
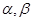 为使互不重合的平面,
为使互不重合的平面,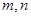 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题:


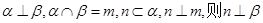 ;
; 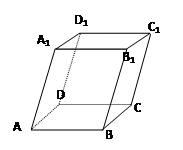
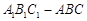 中,侧面
中,侧面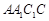
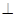 底面ABC,侧面
底面ABC,侧面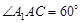 ,E、F分别是
,E、F分别是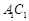 、AB的中点.
、AB的中点.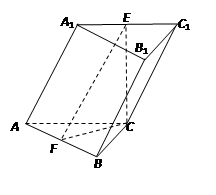
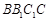 ;
;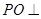 平面
平面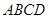 ,点
,点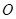 在
在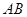 上,
上,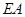 ∥
∥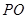 ,四边形
,四边形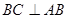 ,
,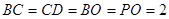 ,
,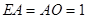
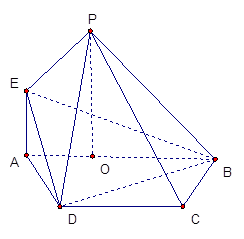
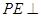 平面
平面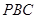 ;
;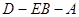 的余弦值;
的余弦值;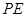 上是否存在点
上是否存在点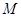 ,使
,使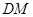 ∥平面
∥平面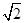 ,F是BC的中点.
,F是BC的中点.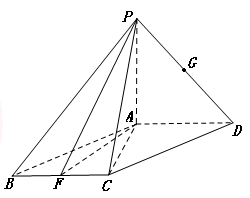
 中,
中, 分别是
分别是 的中点,有下列三个论断:
的中点,有下列三个论断: ;②
;② //平面
//平面 ;③
;③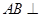 平面
平面