题目内容
集合 ,
, ,
, ,
, ,则集合
,则集合 的个数为( )
的个数为( )
| A.0 | B.2 | C.4 | D.8 |
C
解析试题分析:法一:从0开始逐一验证自然数可知 ,
, ,要使
,要使 ,
, 中必含有元素1,可以有元素2,3,所以
中必含有元素1,可以有元素2,3,所以 只有
只有 .
.
法二:



 ,
,
 =
=
 ,所以集合S中必含元素1,可以是
,所以集合S中必含元素1,可以是 ,共4个.故选
,共4个.故选 .
.
考点:1.分式不等式的解法;2.对数不等式的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若关于 的方程
的方程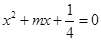 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数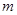 的取值范围是( )
的取值范围是( )
A.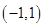 | B.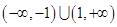 |
C.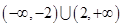 | D.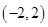 |
不等式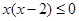 的解集是( )
的解集是( )
A.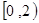 | B.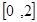 |
C.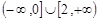 | D.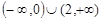 |
已知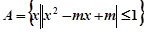 ,若
,若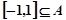 ,则实数
,则实数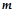 的取值范围为( )
的取值范围为( )
A. | B.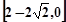 | C.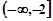 | D. |
关于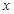 的不等式
的不等式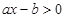 的解集是
的解集是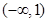 ,则关于
,则关于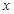 的不等式
的不等式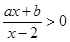 的解为( )
的解为( )
A. | B.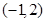 | C.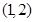 | D.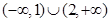 |
设集合 ,
,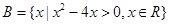 ,则
,则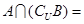 ( )
( )
A.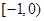 | B.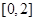 | C.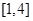 | D. |
不等式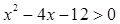 的解集是
的解集是
A.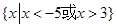 | B.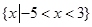 |
C.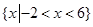 | D.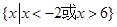 |
若不等式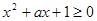 对任意
对任意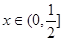 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.0 | B.-2 | C.-3 | D.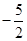 |
不等式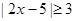 的解集为( )
的解集为( )
A.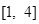 | B.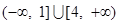 |
C.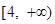 | D.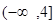 |