Question

【题目】如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（ ）．

A.棱的高与底边长的比为B.侧棱与底面所成的角为

C.棱锥的高与底面边长的比为D.侧棱与底面所成的角为

Answer 1

【答案】AB

【解析】

设四棱锥的高为，底面边长为，由得，然后可得侧面积为，运用导数可求出当时侧面积取得最小值，此时，然后求出棱锥的高与底面边长的比和即可选出答案.

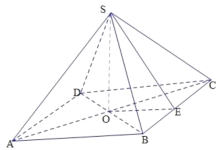
设四棱锥的高为，底面边长为

可得，即

所以其侧面积为

令，则

令得

当时，单调递减

当时，单调递增

所以当时取得最小值，即四棱锥的侧面积最小

此时

所以棱锥的高与底面边长的比为，故A正确，C错误

侧棱与底面所成的角为，由，可得

所以，故B正确，D错误

故选：AB