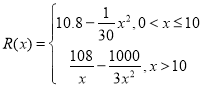题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的最大值;
的最大值;
(2)若函数![]() 与
与![]() 有相同极值点.
有相同极值点.
①求实数![]() 的值;
的值;
②若对于![]() (
(![]() 为自然对数的底数),不等式
为自然对数的底数),不等式![]() 恒成立,
恒成立,
求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)1; (ⅱ)
;(Ⅱ)(ⅰ)1; (ⅱ)![]() .
.
【解析】
试题(1)求导函数,确定函数的单调性,从而得函数![]() 的最大值;(2)(ⅰ)求导函数,利用函数
的最大值;(2)(ⅰ)求导函数,利用函数![]() 与
与![]() 有相同极值点,可得
有相同极值点,可得![]() 是函数
是函数![]() 的极值点,从而求解
的极值点,从而求解![]() 的值;(ⅱ)先求出
的值;(ⅱ)先求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再将对于
,再将对于![]() ,不等式
,不等式![]() 恒成立,等价变形,分类讨论,即可求解实数
恒成立,等价变形,分类讨论,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
∴函数![]() 的最大值为
的最大值为![]() ;
;
(2)∵![]() ,∴
,∴![]() ,
,
(Ⅰ)由(1)知,![]() 是函数
是函数![]() 的极值点,又∵函数
的极值点,又∵函数![]() 与
与![]() 有相同极值点,
有相同极值点,
∴![]() 是函数
是函数![]() 的极值点,∴
的极值点,∴![]() ,解得
,解得![]() ,
,
经检验,当![]() 时,函数
时,函数![]() 取到极小值,符合题意;
取到极小值,符合题意;
(ⅱ)∵![]() ,
,![]() ,
,![]() , ∵
, ∵![]() , 即
, 即![]() ,∴
,∴![]() ,
,![]() ,
,
由(ⅰ)知![]() ,∴
,∴![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 为减函数,在
为减函数,在![]() 上为增函数,∵
上为增函数,∵![]() ,
,
而![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,
①当![]() ,即
,即![]() 时,对于
时,对于![]() ,不等式
,不等式![]() 恒成立
恒成立
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,
,
②当![]() ,即
,即![]() 时,对于
时,对于![]() ,不等式
,不等式![]() ,
,
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
,
∴![]() .综上,所求的实数
.综上,所求的实数![]() 的取值范围为
的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
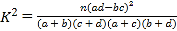 (其中
(其中![]() ).
).
【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: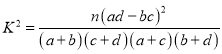
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |