题目内容
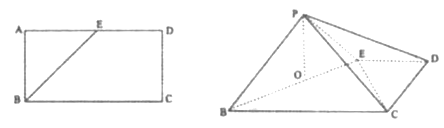
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 丄底面
丄底面![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四棱锥
把四棱锥![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)先证明等腰梯形![]() 中
中![]() ,然后证明
,然后证明![]() ,即可得到
,即可得到![]() 丄平面
丄平面![]() ,从而可证明平面
,从而可证明平面![]() 丄平面
丄平面![]() ;(2)由
;(2)由![]() ,可得到
,可得到![]() ,列出式子可求出
,列出式子可求出![]() ,然后建立如图的空间坐标系,求出平面
,然后建立如图的空间坐标系,求出平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,由
,由 可得到答案。
可得到答案。
(1)证明:在等腰梯形![]() ,
,![]() ,
,
易得![]()
在![]() 中,
中,![]() ,
,
则有![]() ,故
,故![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
即![]() 平面
平面![]() ,故平面
,故平面![]() 丄平面
丄平面![]() .
.
(2)在梯形![]() 中,设
中,设![]() ,
,
![]() ,
,![]() ,
,
![]() ,而
,而![]() ,
,
即![]() ,
,![]() .
.
以点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图的空间坐标系,则
轴,建立如图的空间坐标系,则![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由 得
得 ,
,
取![]() ,得
,得![]() ,
,![]() ,
,
同理可求得平面![]() 的法向量为
的法向量为![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】2020年春节期间,随着新型冠状病毒肺炎疫情在全国扩散,各省均启动重大突发公共卫生事件一级响应,采取了一系列有效的防控措施.如测量体温、有效隔离等.
(1)现从深圳市某社区的体温登记表中随机采集100个样本.据分析,人群体温近似服从正态分布![]() .若
.若![]() 表示所采集100个样本的数值在
表示所采集100个样本的数值在![]() 之外的的个数,求
之外的的个数,求![]() 及X的数学期望.
及X的数学期望.
(2)疫情期间,武汉大学中南医院重症监护室(ICU)主任彭志勇团队对138例确诊患者进行跟踪记录.为了分析并发症(complications)与重症患者(ICU)有关的可信程度,现从该团队发表在国际顶级医学期刊JAMA《美国医学会杂志》研究论文中获得相关数据.请将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.1%的前提下认为“重症患者与并发症有关”?

附:若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式与临界值表: ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品.
内的产品为合格品,否则为不合格品.
注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量(克) | 频数 |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
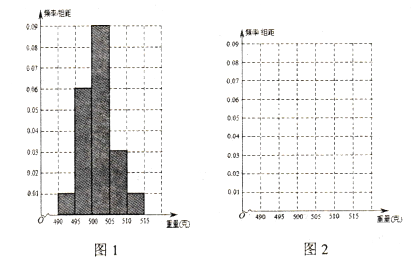
(1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
甲流水线 | 乙流水线 | 合计 | |
合格 | |||
不合格 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |