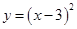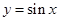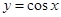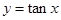题目内容
函数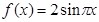 与函数
与函数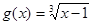 的图像所有交点的橫坐标之和为 .
的图像所有交点的橫坐标之和为 .
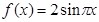 与函数
与函数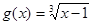 的图像所有交点的橫坐标之和为 .
的图像所有交点的橫坐标之和为 .17
试题分析:分析函数的图象可知,函数
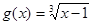 的图像与
的图像与 轴交于点
轴交于点 ,且它的图象关于点
,且它的图象关于点 成中心对称,函数
成中心对称,函数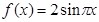 是周期为2的函数,最大值为2,且也关于点
是周期为2的函数,最大值为2,且也关于点 对称(点
对称(点 是它们的唯一一个在
是它们的唯一一个在 轴上的交点),下面我们分析在
轴上的交点),下面我们分析在 时,它们有几个交点,由于
时,它们有几个交点,由于 ,
, ,
, ,故两个函数图象在区间
,故两个函数图象在区间 内有两个交点,当然在区间
内有两个交点,当然在区间 ,
, ,
, 上也分别有两个交点,即在
上也分别有两个交点,即在 时,两函数图象有8个交点,根据对称性,在
时,两函数图象有8个交点,根据对称性,在 时,也有8个交点,而且关于点
时,也有8个交点,而且关于点 对称的两个交点横坐标之和为2,16个交点横坐标之和就是16,所有交点横坐标之和为17.
对称的两个交点横坐标之和为2,16个交点横坐标之和就是16,所有交点横坐标之和为17.
练习册系列答案
相关题目
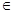 R).
R).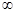 )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;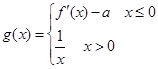 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;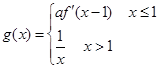 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。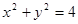 上任取一点
上任取一点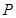 ,设点
,设点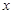 轴上的正投影为点
轴上的正投影为点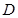 .当点
.当点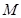 满足
满足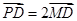 ,动点
,动点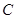 .
.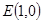 ,若
,若 、
、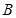 是曲线
是曲线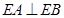 ,求
,求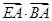 的取值范围.
的取值范围.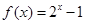 ,对于满足
,对于满足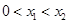 的任意
的任意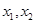 ,下列结论:
,下列结论: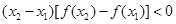 ;(2)
;(2)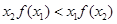
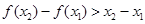 ; (4)
; (4)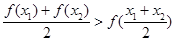
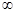 )上单调递减的是( )
)上单调递减的是( ) 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在 上是增函数,则一定有( )
上是增函数,则一定有( )
 ≥
≥

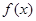 是定义在
是定义在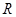 上的偶函数,它在
上的偶函数,它在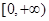 上是减函数,若
上是减函数,若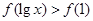 ,则
,则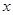 的取值范围是( )
的取值范围是( )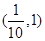
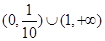
 上为减函数的是( )
上为减函数的是( )