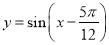题目内容
(本题满分12分)已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)在 中,内角
中,内角 所对边的长分别是
所对边的长分别是 ,若
,若 ,求
,求 的面积
的面积 的值.
的值.
(1)  ;(2)
;(2) .
.
【解析】
试题分析:(1)函数解析式利用二倍角的正弦、余弦函数公式化简,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的单调性即可确定出f(x)的单调递增区间;(2)由已知 及(1)的结论求出角A的大小,再由正弦定理即可求出a边的长度,从而利用公式
及(1)的结论求出角A的大小,再由正弦定理即可求出a边的长度,从而利用公式 就可求出其面积.
就可求出其面积.
试题解析: (1)∵ ,
,
∴ .
.
由 ,解得
,解得 .
.
∴函数 的单调递增区间是
的单调递增区间是 .
.
(2)∵在 中,
中, ,
,
∴ 解得
解得 .
.
又 ,
,
∴ .
.
依据正弦定理,有 .
.
∴ .
.
∴ .
.
考点:1.两角和与差的正弦函数;2. 三角函数的单调性及其求法;3. 正余弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 B.
B. C.
C. D.
D.
 (
( 是虚数单位)的共轭复数为
是虚数单位)的共轭复数为 (B)
(B) (C)
(C) (D)
(D)
 ,
, ,且
,且 ,
, ,则
,则 的值是( )
的值是( ) (B)
(B) (C)
(C) 或
或 (D)
(D) 或
或

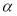 ,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ). 的展开式中第3项的系数是
的展开式中第3项的系数是 ,数列
,数列
 是公差为
是公差为 的等差数列,且前
的等差数列,且前 项和为
项和为 ,则
,则 = .
= . 是
是 的重心,内角
的重心,内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,则角
,则角 的大小是 .
的大小是 .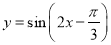 的图象向右平移
的图象向右平移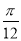 个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为
个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为