题目内容
15.不等式ax2-3ax-6<0的解集为{x|x<1或x>b},则a+b=-1.分析 利用一元二次不等式与对应方程的关系,结合根与系数的关系,即可求出a、b的值.
解答 解:∵不等式ax2-3ax-6<0的解集为{x|x<1或x>b},
∴1,b是方程ax2-3ax-6=0的两实根,
由根与系数的关系得$\left\{\begin{array}{l}{1+b=3}\\{1•b=-\frac{6}{a}}\end{array}\right.$,
解得a=-3,b=2,
∴a+b=-1.
故答案为:-1.
点评 本题主要考察一元二次不等式与一元二次方程之间的关系.解题的关键是一元二次不等式与一元二次方程之间的关系的转化与应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.函数f(x)=|x|+1是( )
| A. | 在(0,+∞)上单调递增的奇函数 | B. | 在(0,+∞)上单调递减的奇函数 | ||
| C. | 在(0,+∞)上单调递增的偶函数 | D. | 在(0,+∞)上单调递减的偶函数 |
3.设数列{an}是等差数列,且a4=-4,a9=4,Sn是数列{an}的前n项和,则( )
| A. | S5<S6 | B. | S5=S6 | C. | S7=S5 | D. | S7=S6. |
10.已知函数h(x)=ax2+bx+c(a≠0)在区间(a,c)上为偶函数,则h(-1)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
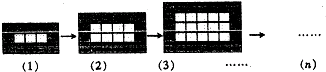

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
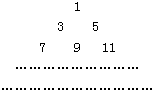 把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表:
把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表: