题目内容
6.函数f(x)=ax+b,(a>0),g(x)=f(x)(x+m),f[f(x)]=16x+5.(1)求f(x)解析式;
(2)当x∈[1,3]时,g(x)有最大值为13,求m的值.
分析 (1)运用待定系数法,由恒等式知识,即可解得a=4,b=1,可得f(x)的解析式;
(2)求出g(x)的对称轴,讨论对称轴和区间的关系,运用单调性,解方程可得m的值.
解答 解:(1)函数f(x)=ax+b,(a>0),
f[f(x)]=a(ax+b)+b=16x+5,
即有a2=16,ab+b=5,解得a=4,b=1,(a=-4,b=-$\frac{5}{3}$舍去),
则f(x)=4x+1;
(2)g(x)=(4x+1)(x+m)=4x2+(4m+1)x+m,
对称轴为x=-$\frac{4m+1}{8}$,
由抛物线开口向上,故最大值,只能为端点的函数值.
若-$\frac{4m+1}{8}$≥3,即为m≤-$\frac{25}{4}$时,区间[1,3]递减,
可得g(1)=13,解得m=$\frac{8}{5}$>-$\frac{25}{4}$,不成立;
若-$\frac{4m+1}{8}$≤1,即为m≥-$\frac{9}{4}$时,区间[1,3]递增,
可得g(3)=13,解得m=-2>-$\frac{9}{4}$,成立.
综上可得,m=-2.
点评 本题考查函数的解析式的求法,注意运用待定系数法,考查二次函数的最值的求法,注意讨论对称轴和区间的关系,考查运算能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.1,log23,log0.53的大小关系是( )
| A. | log23>1>log0.53 | B. | 1>log23>log0.53 | C. | log23>log0.53>1 | D. | log0.53>log23>1 |
15.已知x∈R,m=(x+1)(x2+$\frac{x}{2}$+1),n=(x+$\frac{1}{2}$)(x2+x+1),则m,n的大小关系为( )
| A. | m=n | B. | m>n | C. | m≤n | D. | m<n |
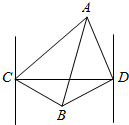 如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).
如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).