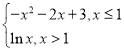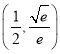题目内容
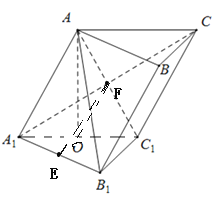
【题目】如图,在斜三棱柱ABC﹣A1B1C1中,点O、E分别是A1C1、A1B1的中点,A1C与AC1交于点F,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
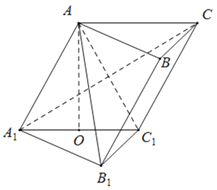
(1)求证:EF∥平面BB1C1C;
(2)求A1C1与平面AA1B1所成角的正弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)推导出OE∥B1C1,OF∥C1C,,从而平面OEF∥平面BB1C1C,由此能证明EF∥平面BB1C1C;
(2)设点C1到平面AA1B1的距离为d,由![]() ,求出
,求出![]() 由此能求出A1C1与平面AA1B1所成角的正弦值.
由此能求出A1C1与平面AA1B1所成角的正弦值.
证明:(1)∵O,E分别是A1C1、A1B1的中点,A1C与AC1交于点F,
∴OE![]() B1C1,OF
B1C1,OF![]() C1C,
C1C,
又![]() 平面BB1C1C,
平面BB1C1C,![]() 平面BB1C1C,
平面BB1C1C,
![]() 平面BB1C1C,
平面BB1C1C,
同理![]() 平面BB1C1C,
平面BB1C1C,
又![]() ,
,![]() 平面OEF,
平面OEF,
∴平面OEF![]() 平面BB1C1C,
平面BB1C1C,
∵EF平面OEF,
∴EF![]() 平面BB1C1C.
平面BB1C1C.
(2)设点C1到平面AA1B1的距离为d,
∵![]() ,
,
∴![]() ,
,
AO![]() ,OB1
,OB1![]() ,
,
AB1![]() 2
2![]() ,
,
∵△AA1B1中,A1B1=AB1=2![]() ,AA=2,
,AA=2,
边AA上的高为:![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得d![]() ,
,
设A1C1与平面AA1B1所成角为θ,
∴A1C1与平面AA1B1所成角的正弦值为:
sinθ![]() .
.

【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35.
地区当中“非常满意”的观众的概率为0.35.
非常满意 | 满意 | 合计 | |
| 30 | 15 | |
|
|
| |
合计 |
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:参考公式:![]() .
.