题目内容
6.将函数$f(x)=sin({4x+\frac{π}{3}})$的图象向左平移φ(φ>0)个单位后关于直线x=$\frac{π}{12}$对称,则φ的最小值为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{24}$ | C. | $\frac{π}{4}$ | D. | $\frac{7π}{24}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,可得$4×\frac{π}{12}+4φ+\frac{π}{3}=\frac{π}{2}+kπ$,k∈Z,由此求得φ的最小值.
解答 解:把函数$f(x)=sin({4x+\frac{π}{3}})$的图象向左平移φ(φ>0)个单位后,可得y=sin[4(x+φ)+$\frac{π}{3}$]=sin(4x+4φ+$\frac{π}{3}$)的图象,
由于所得图象关于直线$x=\frac{π}{12}$对称,
∴$4×\frac{π}{12}+4φ+\frac{π}{3}=\frac{π}{2}+kπ$,∴$φ=\frac{kπ}{4}-\frac{π}{24}({k∈Z})$,
∵φ>0,∴${φ_{min}}=\frac{5π}{24}$,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
1.已知某随机变量X的概率密度函数为$P(x)=\left\{\begin{array}{l}0,x≠0\\{e^{-x}},x>0\end{array}\right.$,则随机变量X落在区间(1,3)内的概率为( )
| A. | $\frac{e+1}{e^2}$ | B. | $\frac{{{e^2}-1}}{e^3}$ | C. | e2-e | D. | e2+e |
11.已知命题p:若x<-3,则x2-2x-8>0,则下列叙述正确的是( )
| A. | 命题p的逆命题是:若x2-2x-8≤0,则x<-3 | |
| B. | 命题p的否命题是:若x≥-3,则x2-2x-8>0 | |
| C. | 命题p的否命题是:若x<-3,则x2-2x-8≤0 | |
| D. | 命题p的逆否命题是真命题 |
18.设$a=(\frac{7}{9})^{5}$,$b=(\frac{9}{7})^{\frac{1}{5}}$,$c=lo{g}_{2}\frac{7}{9}$,则a,b,c的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
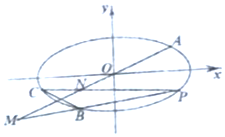 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.