题目内容
12.若曲线y=$\sqrt{1-(x-a)^{2}}$与直线y=x+2有且只有一个公共点,则a的取值范围是-3≤a<1或a=-2+$\sqrt{2}$.分析 曲线y=$\sqrt{1-(x-a)^{2}}$即 (x-a)2+y2=1(y≥0),表示以(a,0)为圆心,半径等于1的上半圆,利用圆心到直线的距离等于半径,即可得出结论.
解答 解:曲线y=$\sqrt{1-(x-a)^{2}}$即 (x-a)2+y2=1(y≥0),表示以(a,0)为圆心,半径等于1的上半圆.
∵曲线y=$\sqrt{1-(x-a)^{2}}$与直线y=x+2有且只有一个公共点,
∴圆心到直线的距离d=$\frac{|a+2|}{\sqrt{2}}$=1,∴a=-2±$\sqrt{2}$,
结合题意,-3≤a<1或a=-2+$\sqrt{2}$
故答案为-3≤a<1或a=-2+$\sqrt{2}$.
点评 本题主要直线与圆的位置关系的运用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
 ,且
,且 ,则当
,则当 的最小值为
的最小值为 时,不等式
时,不等式 解集为_________.
解集为_________. 的面积为
的面积为 ,三内角
,三内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .若
.若 ,则
,则 取最大值时
取最大值时 .
.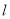 的参数方程式
的参数方程式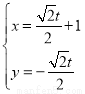 (
(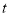 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,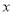 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆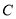 的极坐标方程为
的极坐标方程为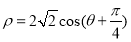 .
.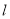 的普通方程与圆
的普通方程与圆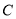 的直角坐标方程;
的直角坐标方程;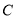 与直线
与直线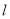 交于
交于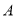 、
、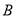 两点,若
两点,若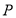 点的直角坐标为
点的直角坐标为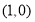 ,求
,求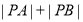 的值.
的值.