题目内容
9.△ABC的内角A、B、C的对边分别为a、b、c,已知2a=$\sqrt{3}$csinA-acosC.(1)求C;
(2)若c=$\sqrt{3}$,求△ABC的面积S的最大值.
分析 (1)由正弦定理,三角函数恒等变换的应用化简已知等式可得sin(C-$\frac{π}{6}$)=1,结合C的范围,可得C的值.
(2)由余弦定理,基本不等式可求ab≤1,进而利用三角形面积公式可求△ABC面积的最大值.
解答 (本题满分为12分)
解:(1)∵2a=$\sqrt{3}$csinA-acosC,
∴由正弦定理可得:2sinA=$\sqrt{3}$sinCsinA-sinAcosC,…2分
∵sinA≠0,
∴可得:2=$\sqrt{3}$sinC-cosC,解得:sin(C-$\frac{π}{6}$)=1,
∵C∈(0,π),可得:C-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
∴C-$\frac{π}{6}$=$\frac{π}{2}$,可得:C=$\frac{2π}{3}$.…6分
(2)∵由(1)可得:cosC=-$\frac{1}{2}$,
∴由余弦定理,基本不等式可得:3=b2+a2+ab≥3ab,即:ab≤1,(当且仅当b=a时取等号)…8分
∴S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab≤$\frac{\sqrt{3}}{4}$,可得△ABC面积的最大值为$\frac{\sqrt{3}}{4}$.…12分
点评 本题主要考查了正弦定理,两角和的正弦函数公式,余弦定理,基本不等式,三角形面积公式在解三角形中的综合应用,考查了转化思想,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
14.欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将复数、指数函数与三角函数联系起来,将指数函数的定义域扩充为复数,它在复变函数论里占有非常重要的地位,被誉为“数学中的天骄”,根据欧拉公式可知,复数e-2i所对应的点在复平面中位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16. 某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
 某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )| A. | 46,45 | B. | 45,46 | C. | 45,45 | D. | 47,45 |
 的三个内角为
的三个内角为 ,若
,若 ,求
,求 的最大值.
的最大值.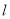 的参数方程式
的参数方程式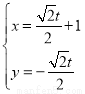 (
(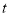 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,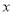 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆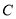 的极坐标方程为
的极坐标方程为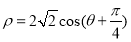 .
.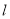 的普通方程与圆
的普通方程与圆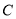 的直角坐标方程;
的直角坐标方程;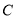 与直线
与直线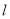 交于
交于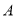 、
、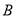 两点,若
两点,若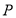 点的直角坐标为
点的直角坐标为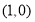 ,求
,求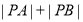 的值.
的值.