题目内容
2.设函数f(x)=ax2-bx+3,且f(x)>0的解集为(-1,3),(1)求函数f(x)的表达式;
(2)设g(x)=$\frac{f(x)}{x}$,若g(3+2sinθ)≥$\frac{1}{5}$m2-$\frac{12}{5}$m对任意θ∈R恒成立,则实数m的取值范围.
分析 (1)根据方程和一元二次不等式的解集的关系,根据韦达定理即可求出a,b的值,继而求出函数f(x)的解析式,
(2)先求出3+2sinθ的范围,根据g(x)的单调性质,求出g(3+2sinθ)min=g(5)=-$\frac{12}{5}$,继而得到关于m的不等式,解得即可.
解答 解:(1)由题知:方程ax2-bx+3=0的解为-1与3,
则$\left\{\begin{array}{l}{-1+3=\frac{b}{a}}\\{-1×3=\frac{3}{a}}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$,
∴f(x)=-x2+2x+3,
(2)由(1)g(x)=$\frac{f(x)}{x}$=$\frac{3}{x}$-x+2,
∵θ∈R,
∴-1≤sinθ≤1,
∴1≤3+2sinθ≤5,
∵g(x)是单调减函数,
∴g(3+2sinθ)min=g(5)=-$\frac{12}{5}$,
∴$\frac{1}{5}$m2-$\frac{12}{5}$m≤-$\frac{12}{5}$
即:m2-12m+12≤0,
解得6-2$\sqrt{6}$≤m≤6+2$\sqrt{6}$,
∴实数m的取值范围为[6-2$\sqrt{6}$,6+2$\sqrt{6}$].
点评 本题考查了一元二次不等式和函数解析式的求法,以及解决不等式恒成立问题,通过转化为函数最值问题来解决是常用的方法.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
13.下列各函数中,为指数函数的是( )
| A. | y=(-1.3)x | B. | y=${(\frac{1}{2})}^{x}$ | C. | y=x2 | D. | y=x-1 |
7.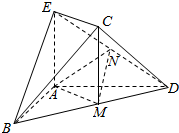 如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
 如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
14.已知数列{bn}中,b1=4,且bn+1-2bn-4=0,则b8=( )
| A. | 28-4 | B. | 210-4 | C. | 212-4 | D. | 29-4 |