题目内容

精英家教网函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π2
)的部分图象如图所示，则f（x）=
 
．
分析：由函数的图象顶点的纵坐标求出A，根据半个周期
T
2
=
π
ω
=6-2=4，求出ω，根据（
π
4
×0+∅）=0求出∅值．
解答：解：根据图象顶点的纵坐标可得A=2，
T
2
=
π
ω
=6-2=4，∴ω=
π
4
，故函数为y=2sin（
π
4
 x+∅），
由五点法作图可得（
π
4
×0+∅）=0，∴∅=0，故f（x）=2sin
π
4
x，
故答案为2sin
π
4
 x．
点评：本题考查由函数 y=Asinn（ωx+∅）的部分图象求出其解析式的方法，体现了数形结合的数学思想．
练习册系列答案
相关题目
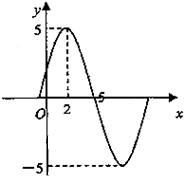精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）若图象g（x）与函数f（x）的图象关于点P（4，0）对称，求函数g（x）的单调递增区间．
（2013•大连一模）已知函数f(x)=Asin(ωx+φ)(x∈R，A＞0，ω＞0，|φ|＜
π
2
)的图象（部分）如图所示，则ω，φ分别为（　　）
当x∈[-
π
6
，
2π
3
]时，函数f(x)=Asin(ωx+θ) (A＞0，ω＞0，|θ|＜
π
2
)的图象如图所示．
（1）求函数f（x）在[-
π
6
，
2π
3
]上的表达式；
（2）求方程f(x)=
2
2
在[-
π
6
，
2π
3
]的解集．
精英家教网函数f(x)=Asin(ωx+φ)，x∈R(A＞0，ω＞0，|φ|＜
π
2
)的一段图象如图5所示：将y=f（x）的图象向右平移m（m＞0）个单位，可得到函数y=g（x）的图象，且图象关于原点对称，g(
π
2013
)＞0．
（1）求A、ω、φ的值；
（2）求m的最小值，并写出g（x）的表达式；
（3）若关于x的函数y=g(
tx
2
)在区间[-
π
3
，
π
4
]上最小值为-2，求实数t的取值范围．
精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，x∈R，|φ|＜
π
2
)的图象（部分）如图所示，则f（x）的解析式是（　　）
A、f(x)=5sin(
π
3
x+
π
6
)
B、f(x)=5sin(
π
6
x-
π
6
)
C、f(x)=5sin(
π
6
x+
π
6
)
D、f(x)=5sin(
π
3
x-
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网