题目内容
设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试判断函数f(x)的单调性,并求使不等式f(sin2θ+cos2θ)+f(1﹣tcosθ)<0对所有的θ∈(0,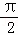 )均成立的t的取值范围;
)均成立的t的取值范围;
(2)若f(1)=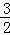 ,g(x)=a2x+a﹣2x﹣2mf(x),且g(x)在[1,+∞)上的最小值为﹣1,求m的值.
,g(x)=a2x+a﹣2x﹣2mf(x),且g(x)在[1,+∞)上的最小值为﹣1,求m的值.
解:(1)∵函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
∴f(0)=0,
∴1﹣(k﹣1)=0,
解得k=2,
∴f(x)=ax ﹣a﹣x,
﹣a﹣x,
∵f(1)=a﹣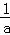 >0,且a>0且a≠1,
>0,且a>0且a≠1,
∴a>1,
∴f(x)是定义域为R的奇函数且单调递增,
∵f(sin2θ+cos2θ)+f(1﹣tcosθ)<0对所有的θ∈(0,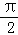 )均成立,
)均成立,
∴sin2θ+cos2θ+1﹣tcosθ<0,
即tcosθ>sin2θ+cos2θ+1=2sinθcosθ+2cos2θ,
∵θ∈(0,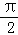 ),
),
∴cosθ(0,1),
则t>2sinθ+2cosθ=2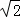 sin(θ+
sin(θ+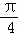 ),
),
又当θ=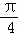 时,2
时,2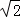 sin(θ+
sin(θ+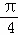 )的最大值为2
)的最大值为2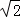 ,
,
∴t>2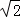 ,
,
∴t的取值范围为(2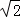 ,+∞);
,+∞);
(Ⅱ)由(1)知,f(x)=ax﹣a﹣x,
∵f(1)=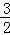 ,
,
∴a﹣ =
=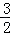 ,解得a=2.
,解得a=2.
故f(x)=2x﹣2﹣x,g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x),
令t=2x﹣2﹣x,则22x+2﹣2x=t2+2,由x∈[1,+∞),得t∈[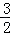 ,+∞),
,+∞),
∴g(x)=h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2,t∈[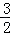 ,+∞),
,+∞),
当m≥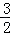 时,当t=m时,h(t)min=2﹣m2=﹣1,解得m=
时,当t=m时,h(t)min=2﹣m2=﹣1,解得m=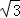 ,或m=
,或m=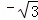 (舍去),
(舍去),
当m<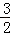 时,当t=
时,当t=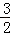 ,h(t)min=
,h(t)min= ﹣3m=1,解得m=
﹣3m=1,解得m=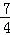 (舍去).
(舍去).
综上,m的值是2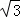 .
.

练习册系列答案
相关题目
 ”是“函数
”是“函数 上是增函数”的
上是增函数”的 ,则x的取值范围是()
,则x的取值范围是()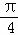 +kπ,
+kπ, +kπ](k∈Z)
+kπ](k∈Z) +2kπ,
+2kπ, +2kπ](k∈Z)
+2kπ](k∈Z)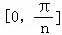 上的面积为
上的面积为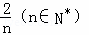 ,则函数y=sin(3x﹣π)+1在
,则函数y=sin(3x﹣π)+1在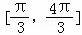 上的面积为.
上的面积为. 上单调递减的函数是 ( )
上单调递减的函数是 ( )  B.
B. C.
C.  D.
D.
 B.
B.
 D.
D.
 ,则符合条件的质数p的个数为 【 】
,则符合条件的质数p的个数为 【 】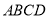 中,
中,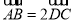 ,
,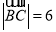 ,
,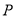 为梯形
为梯形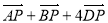 =0,
=0,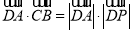 ,
,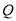 为边
为边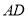 上的一个动点,则
上的一个动点,则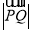 的最小值为 .
的最小值为 .