题目内容
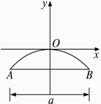
一辆卡车高3米,宽1.6米,欲通过断面为抛物线型的隧道, 已知拱口宽恰好是拱高的4倍,若拱口宽为a米,求使卡车通过的a的最小整数值.解:以隧道顶点为原点,拱高所在直线为y轴建立直角坐标系,则B点的坐标为(
,
),如下图所示.
设隧道所在抛物线方程为x2=my,则(
)2=m·(
),∴m=-a,即抛物线方程为x2=-ay.
将(0.8,y)代入抛物线方程,得
0.82=-ay,即y=-
.?
欲使卡车通过隧道,应有y-(
)>3,
即
.由于a>0,得上述不等式的解为a>12.21.
∴a应取13.
点评:把实际问题转化为数学问题,利用数学模型,通过数学语言(文字,符号,图形,字母等)表达,分析,解决问题,是现代中学生必须具备的能力.
练习册系列答案
相关题目