题目内容
10.等差数列{an}的前n项和为Sn,a3=3,S4=10,则 $\sum_{k=1}^{n}$$\frac{1}{{S}_{k}}$=$\frac{2n}{n+1}$.分析 利用已知条件求出等差数列的前n项和,然后化简所求的表达式,求解即可.
解答 解:等差数列{an}的前n项和为Sn,a3=3,S4=10,S4=2(a2+a3)=10,
可得a2=2,数列的首项为1,公差为1,
Sn=$\frac{n(n+1)}{2}$,$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$,
则 $\sum_{k=1}^{n}$$\frac{1}{{S}_{k}}$=2[1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$]=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$.
故答案为:$\frac{2n}{n+1}$.
点评 本题考查等差数列的求和,裂项消项法求和的应用,考查计算能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
5.若双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2,则C的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
15.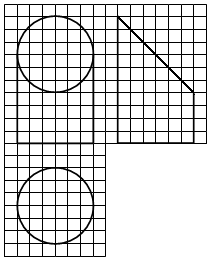 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )| A. | 90π | B. | 63π | C. | 42π | D. | 36π |
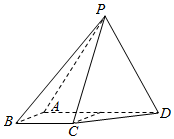 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.